в угол,величина которого равна 60°, вписано две окружности,которые внешне касаются друг друга. Найдите радиус меньшего из них,если радиус большего равен 12 см

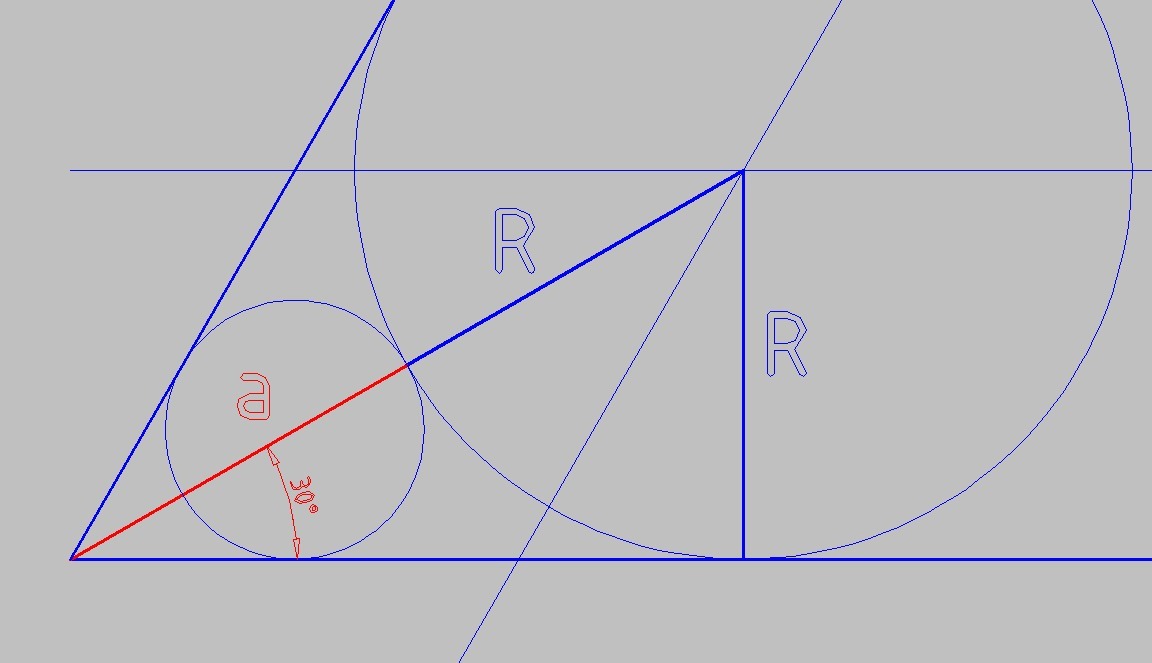
Рассмотрим прямоугольный треугольник, образованный биссектрисой угла в 60°, радиусом большой окружности и нижней стороной угла в 60°
Катет против угла в 30° в этом треугольнике - это радиус большой окружности R = 12 см
Гипотенуза в 2 раза больше, 2R = 24 см
Красная часть гипотенузы, находящаяся вне большой окружности равна 2R - R = R = 12 см
На этом красном отрезке должны разместиться 2 радиуса (r) малой окружности, и остаться свободная часть угла, которая равна радиусу малой окружности
R = r + 2r = 3r
r = R/3 = 12/3 = 4 см