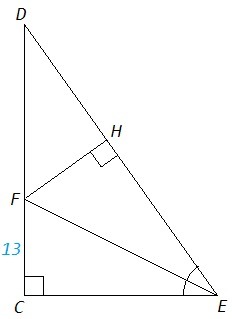
В прямоугольном треугольнике DCE с прямым углом C проведена биссектриса EF, причём FC = 13 см. Найдите растояние от точки F до прямой DE.

∠FHE=90° (FH - расстояние от точки F до прямой DE)
∠HEF=∠CEF (EF - биссектриса ∠E)
△FHE=△FCE (по острому углу и гипотенузе)
FH=FC =13 (см)

ИЛИ

Угол FCE прямой, следовательно FC - расстояние от точки F до CE. Любая точка биссектрисы угла равноудалена от его сторон. Расстояние от F до DE равно расстоянию от F до CE, то есть 13 см.