Предмет: Математика, автор: qwertyru2

Решить уравнение:

Надеюсь на фото всё видно.

Приложения:

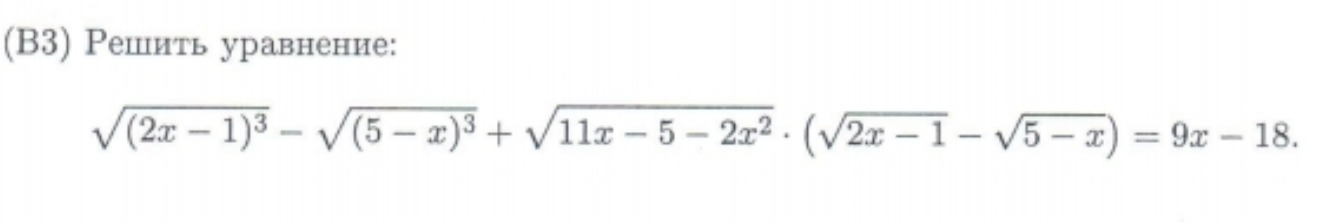
Ответы

Автор ответа: LFP

с помощью удобной замены можно упростить левую часть уравнения...

Приложения:

qwertyru2: Насчёт замены запутался клгда решал,а так да видно что слева в кубе а с права без степени.Большущее спасибо.

LFP: рада была помочь))

Автор ответа: Guerrino

$\sqrt{(2x-1)^{3}}-\sqrt{(5-x)^{3}}+\sqrt{(x-5)(1-2x)}(\sqrt{2x-1}-\sqrt{5-x} =9(x-2)$ ; Чтоб не запутаться в больших выражениях сделаем замену: $2x-1=u, \; 5-x=v$ ; Перепишем: $\sqrt{u^{3}}-\sqrt{v^{3}}+\sqrt{u^{2}v}-\sqrt{uv^{2}}=2(3-v)$ ; Заметим, что при раскрытии скобок в изначальном уравнении под корнем произведение минус-квадрата и выражения x-5 или 1-2x; т.е уравнение имеет корни только тогда, когда u и v положительны. Учтем это при раскрытии корня. $\sqrt{u^{2}u}-\sqrt{v^{2}v}+\sqrt{u^{2}v}-\sqrt{uv^{2}}=9(3-v)\Leftrightarrow u\sqrt{u}-v\sqrt{v}+u\sqrt{v}-v\sqrt{u}=9(3-v)\Leftrightarrow u(\sqrt{u}+\sqrt{v)}-v( \sqrt{u}+\sqrt{v})=9(3-v)\Leftrightarrow (\sqrt{u}+\sqrt{v})(u-v)=9(3-v)$ ; Также, $u-v=3(3-v)$ ; Тогда $3(\sqrt{u}+\sqrt{v})(3-v)=9(3-v)\Leftrightarrow (3-v)(3(\sqrt{u}+\sqrt{v})-2)=0$ ; Решим первое уравнение: 3-v=0 ⇔ v=3; Делаем обратную замену: 5-x=3⇔x=2; $\sqrt{u}+\sqrt{v}=3$ ; Здесь очевидно решение: v=4, u=1, откуда x=1; И u=9, v=0, x=5