Предмет: Геометрия, автор: alexstepanovo

Розв'язать рівняння

Приложения:

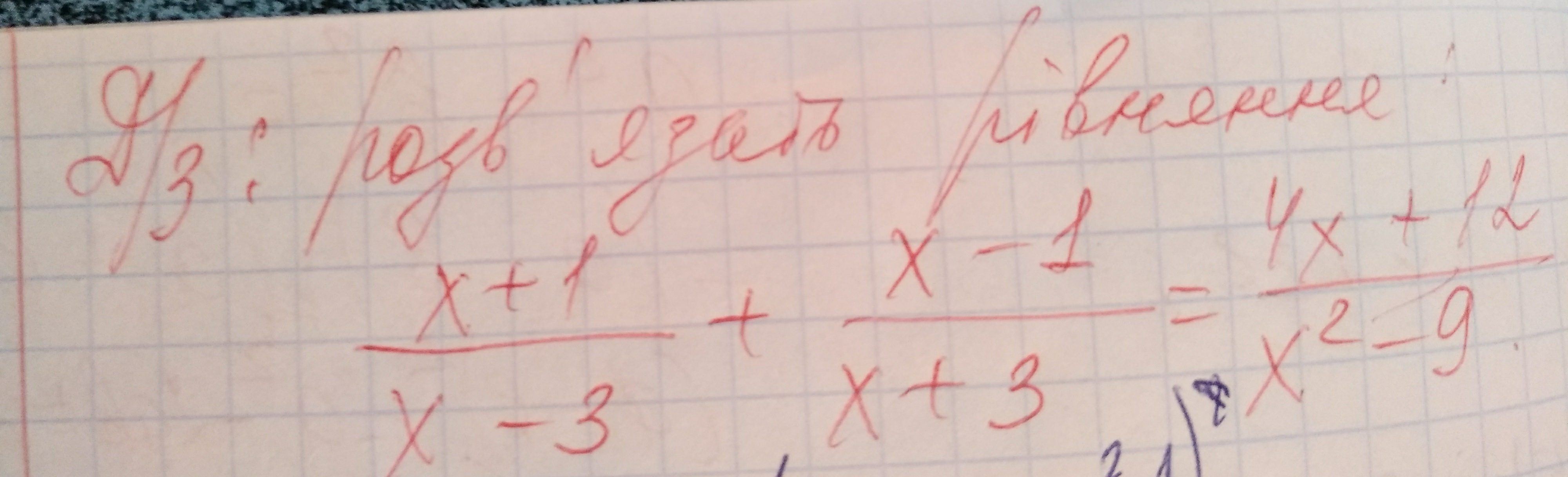
Ответы

Автор ответа: snow99

$\frac{x + 1}{ x - 3 } + \frac{x - 1}{x + 3} = \frac{4x + 12}{ {x}^{2} - 9} \\ \frac{(x + 1)(x + 3) + (x - 1)(x - 3) - 4x - 12}{(x -3)(x + 3) } = 0 \\ \frac{ {x}^{2} + x + 3x + 3 + {x}^{2} - x - 3x + 3 - 4x - 12}{(x - 3)(x + 3)} = 0 \\ \frac{2 {x}^{2} - 4x - 6}{(x - 3)(x + 3)} = 0 \\ \frac{ {x}^{2} - 2x - 3 }{(x - 3)(x + 3)} = 0$
x^2 - 2x - 3 = 0
D = b^2 - 4ac = 4 - 4*(-3) = 16
x1 = (2+4)/2 = 3
x2 = (2-4)/2 = -1
x^2 - 2x - 3 = (x + 1)*(x - 3) = 0

x не равно +-3

Ответ: -1.

Автор ответа: siestarjoki

ОДЗ: x≠3; x≠-3

(x+1)/(x-3) + (x-1)/(x+3) = (4x+12)/(x^2 -9) <=>

(x+1)(x+3) + (x-1)(x-3) - 4(x+3) =0 <=>

(x+1-4)(x+3) + (x-1)(x-3) =0 <=>

(x-3)(x+3) + (x-1)(x-3) =0 <=>

(x-3)(x+3+x-1) =0 <=>

(x-3)(2x+2) =0 <=>

2(x-3)(x+1) =0 <=>

x=-1

Предыдущий вопрос

Следующий вопрос