Предмет: Геометрия,
автор: HopeND
HELP!!!
Решите задачу:
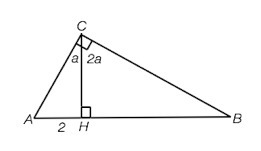
Высота прямоугольного треугольника, опущенная на гипотенузу, делит угол в отношении 1:2 и отсекает от гипотенузы меньший отрезок 2 см. Найти площадь треугольника.
Ответы
Автор ответа:
1
Примем меньшую часть, на которую высота делит прямой угол С треугольника АВС, равной а. Тогда вторая равна 2а.
а+2а=90°
а=90°:3=30°,
2а=2•30°=60°
В ∆ АСН гипотенуза АС вдвое длиннее катета АН, который лежит против угла 30° (свойство). АС=4 см.
Высота прямоугольного треугольника делит его на два подобных друг другу и исходному треугольнику.
∠САВ= ∠ВСН=60°
∠СВН=∠АСН=30°. ⇒
Гипотенуза АВ =2АС=8 см
Высоту СН можно найти по т.Пифагора или
СН=АС•sinCAH=4•√3/2=2√3
S(ABC)=AB•CH:2=(8•2√3):2=8√3см²
Приложения:
Интересные вопросы
Предмет: Литература,
автор: kaede2009
Предмет: Геометрия,
автор: viktoriapopova210
Предмет: Биология,
автор: bogdan2288848
Предмет: Литература,
автор: nataliaно