Предмет: Алгебра, автор: natka5natka

Срочно!!!!Очень-очень срочно! При каких значениях параметра a неравенство: 2-x^2(эта запись под корнем)>a+x имеет решения?

Ответы

Автор ответа: GeniusEnstein

При каких значениях параметра a неравенство $\sqrt{2-x^{2}}>a+x$ имеет решения?

ограничения на x: $x^{2}<2; x>-a$

пусть $f(x)=\sqrt{2-x^{2}}$ , тогда:

$f(x)\geq 0, (f(x))^{2}-(2-x^{2})=0$

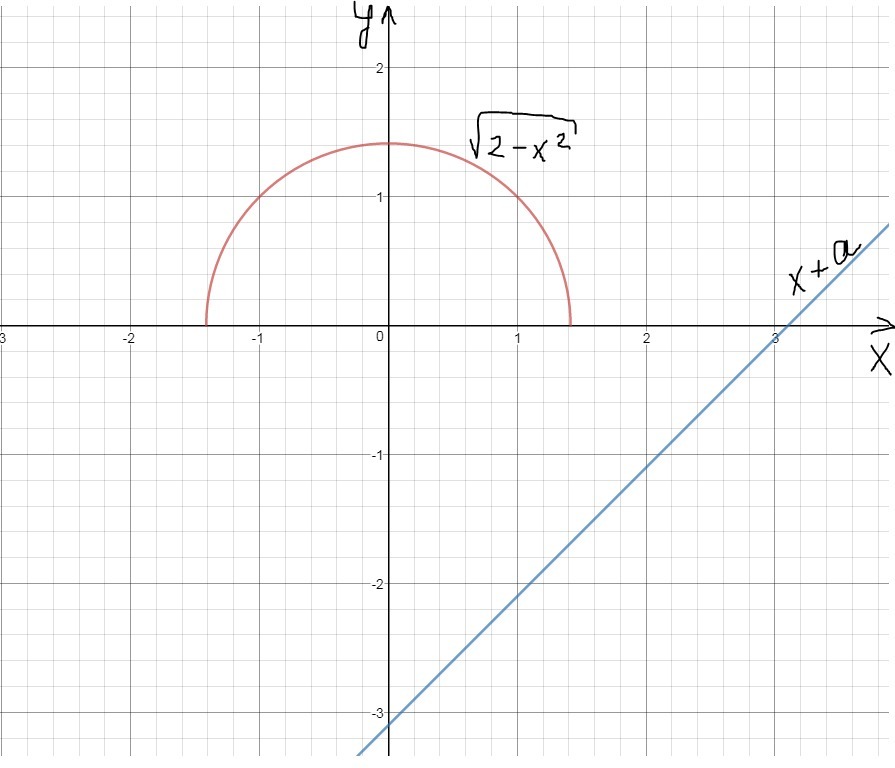
$(f(x))^{2}+x^{2})=(\sqrt{2})^{2}$ - график полуокружности, лежащей выше оси x с центром (0;0) и радиусом $\sqrt{2}$

пусть $g(x)=x+a$ - график прямой, проходящей через (0; a), т.е. $y=x$ смещённый на a вверх-вниз

См. вложения (красным цветом - $f(x)$ , синим цветом - $g(x)$ )

график $g(x)$ должен находиться ниже графика $f(x)$

При $a \to -\infty$ всегда найдётся такой x, что $g(x)<f(x)$

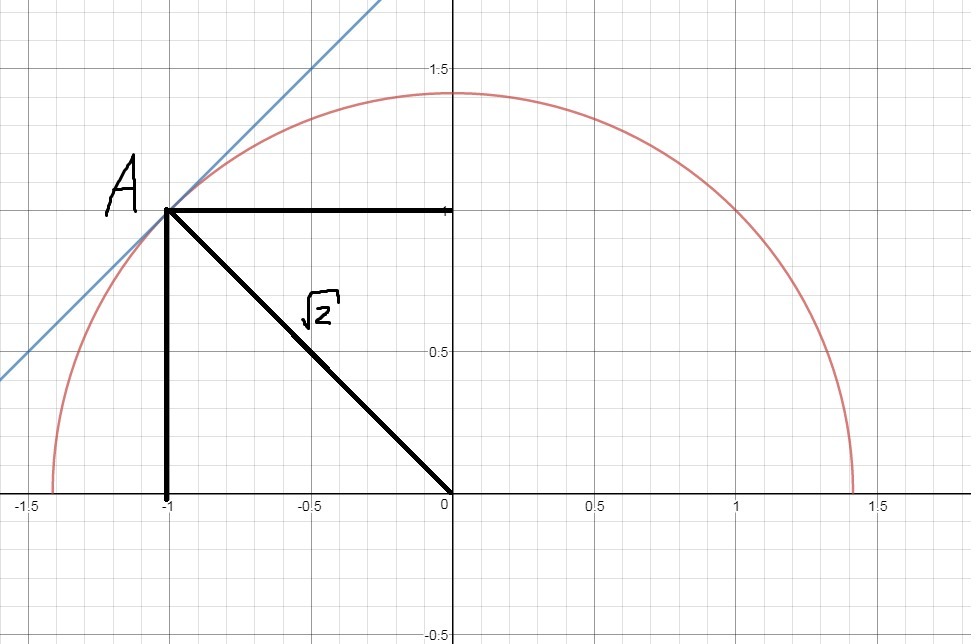
Так будет до касания верхней части окружности (рис.2)

Определим точку касания A:

Её координаты (-1;1), а значит график функции $g(x)$ имеет вид $g(-1)=1; 1=-1+a; a=2$

Следовательно при всех a<2 $g(x)<f(x)$ имеет решения

Ответ: $a<2$

Приложения:

Интересные вопросы

Предмет: Математика, автор: madinabonukhamrakulo

6 лет назад

Предмет: География, автор: zeikanmaria95

6 лет назад

Предмет: География, автор: amethystwitch22

6 лет назад

Предмет: Биология, автор: crafthop2121

9 лет назад

Предмет: Геометрия, автор: VIP111202

9 лет назад