Предмет: Информатика, автор: Dragun228

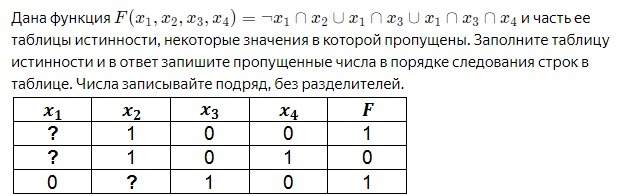
Задача с таблицей истинности, ответ 011, мне нужно только подробное решение!

Приложения:

Ответы

Автор ответа: krenovut

Берем и подставляем.

$F = 1 \Rightarrow \\ 1 = \lnot x1 \cap 1 \cup x1 \cap 0 \cup x1 \cap 0 \cup 0 \\ X \cap 1 = X \\ X \cap 0 = 0 \Rightarrow \\ 1 = \lnot x1 \cup 0\cup 0 \cup 0 \\ \cup = or \Rightarrow \\ 1 = \lnot x1 \cup 0 \\ x1 = 0 \Rightarrow \lnot x1 = 1 \Rightarrow \\ 1 = 1\cup 0 \Rightarrow 1 = 1 $

И так далее Подставляем, сокращаем и получаем то что нужно. Знать надо обычные правила преобразования логических выражений.

Во второй строке получаем все тоже самое, но $F = 0$ . Больше там ничего не меняется, следовательно $x1 = 1$

$F = 1 \Rightarrow \\ 1 = 1 \cap x2 \cup 0 \cap 0 \cup 0 \cap 0 \cup 0 \\ X \cap 1 = X \\ X \cap 0 = 0 \Rightarrow \\ 1 = x2 \cup 0\cup 0 \cup 0 \\ \cup = or \Rightarrow \\ 1 = x2 \cup 0 \\ x2 = 1 \Rightarrow 1 = 1$

Автор ответа: DonPedro80

Для начала попытаемся функцию упростить.

$\lnot x_1\land x_2\lor x_1 \land x_3\lor x_1\land x_3\land x_4=\overline{x_1}x_2+x_1x_3+x_1x_3x_4=\\ \overline{x_1}x_2+x_1x_3(1+x_4)=\overline{x_1}x_2+x_1x_3$