Предмет: Геометрия,
автор: Купальник
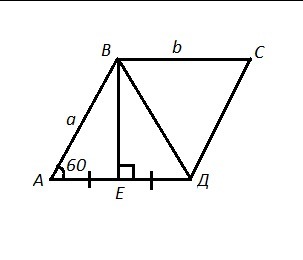
В параллелограмме ABCD угол А равен 60°. Высота ВЕ делит сторону AD на две равные части. Найдите длинну диагонали BD, если периметр параллелограмма равен 48 см
Ответы
Автор ответа:
1068
АВСД - параллелограмм , ∠А=60° , Р=48 см , ВЕ⊥АД , АЕ=ЕД .
Периметр параллелограмма Р=2·(a+b)=48 ⇒ a+b=24 .
АД+АВ=24 см.
Так как ВЕ - высота и АЕ=ЕД , то ΔАВД - равнобедренный: АВ=ВД .
Так как в равнобедренном ΔАВС один из углов равен 60°, то ΔАВС - равносторонний ⇒ АВ=ВД=АД ⇒ АД+АВ=2·АВ=24 , АВ=24:2=12 .
Диагональ ВД=АВ=12 см .
Приложения:
YoWindow4:
спасио ты лучший
спасибо большое
спасибо огромное
Интересные вопросы
Предмет: Математика,
автор: dotsenko9520325
Предмет: Математика,
автор: ovsienko30
Предмет: Английский язык,
автор: diana5164
Предмет: Математика,
автор: ВладимирШ
Предмет: Физика,
автор: istambulova2004