Предмет: Алгебра,
автор: kisonix
Решить уравнение, найти сумму положительных корней.
Приложения:
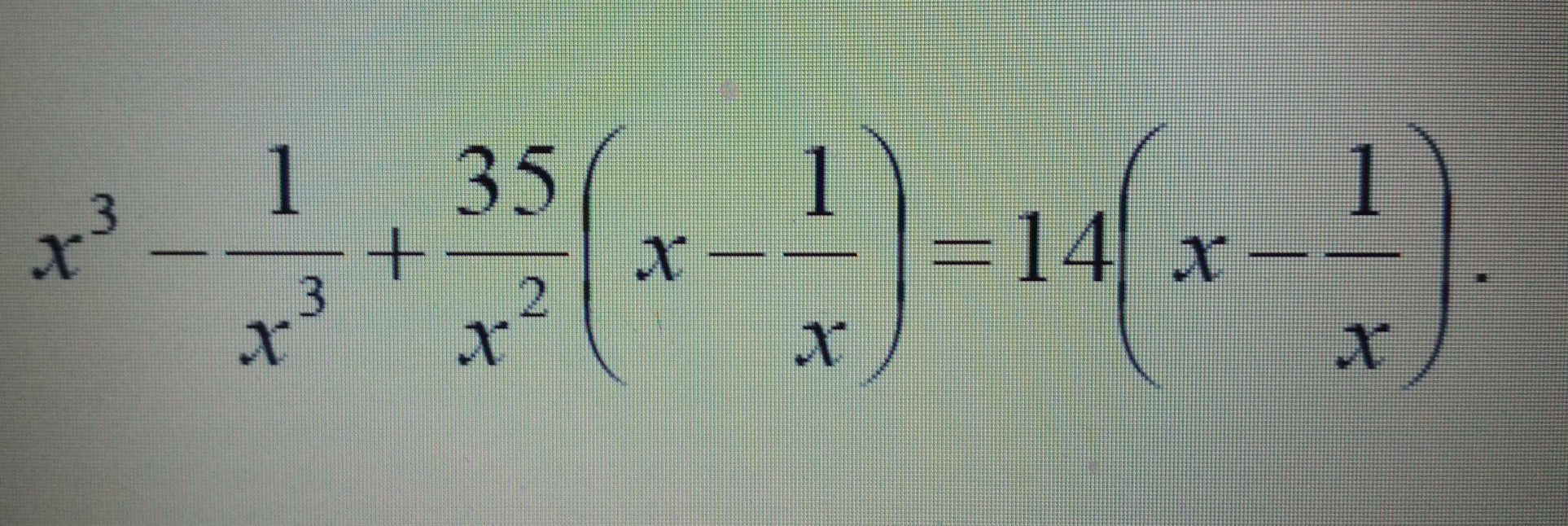
Ответы
Автор ответа:
1
Решение задания приложено
Приложения:

Автор ответа:
0
х^3-1/х^3+(35/х^2)(х-1/х)=14(х-1/х)
(х-1/х)(х^2+1+1/х^2)+(35/х^2)(х-1/х)-14(х-1/х)=0
(х-1/х)(х^2+1+1/х^2+35/х^2-14)=0
(х-1/х)(х^2-13+36/х^2)=0
1) х-1/х=0 |*х
(х^2-1)/х=0
D(y): x≠0
(x-1)(x+1)=0
x={-1; 1}
2) x^2-13+36/x^2=0 |*x^2
x^4-13x^2+36=0
Введем замену: х^2=t, t≥0
t^2-13t+36=0
t=4,
t=9;
Вернёмся к замене:
х^2=4,
х^2=9;
х={-3; -2; 2; 3}
S корней>0=1+2+3=6
Ответ: {-3; -2; -1; 1; 2; 3}; S корней>0=6
(х-1/х)(х^2+1+1/х^2)+(35/х^2)(х-1/х)-14(х-1/х)=0
(х-1/х)(х^2+1+1/х^2+35/х^2-14)=0
(х-1/х)(х^2-13+36/х^2)=0
1) х-1/х=0 |*х
(х^2-1)/х=0
D(y): x≠0
(x-1)(x+1)=0
x={-1; 1}
2) x^2-13+36/x^2=0 |*x^2
x^4-13x^2+36=0
Введем замену: х^2=t, t≥0
t^2-13t+36=0
t=4,
t=9;
Вернёмся к замене:
х^2=4,
х^2=9;
х={-3; -2; 2; 3}
S корней>0=1+2+3=6
Ответ: {-3; -2; -1; 1; 2; 3}; S корней>0=6
Интересные вопросы
Предмет: Биология,
автор: Crabchips
Предмет: Русский язык,
автор: violettanekrasova02
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: demaguzel
Предмет: Математика,
автор: taraLisamailru