Предмет: Математика, автор: juliarosenberg0

Решите пожалуйста: (x+3/x^2-3x+12/9-x^2)*3x/x-3

Ответы

Автор ответа: Единорожек34

Решение во вложении.

Приложения:

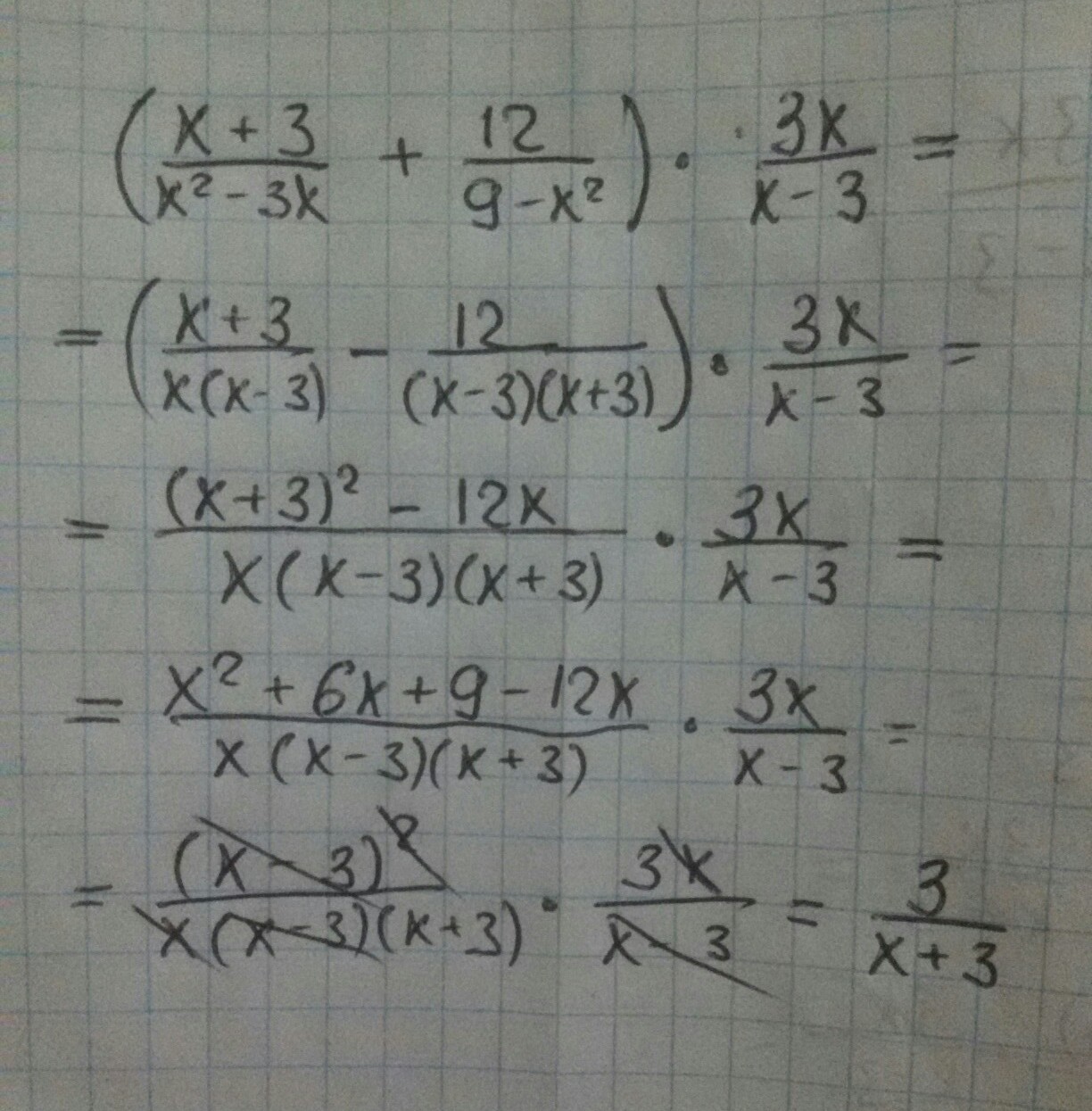
Автор ответа: mishka19

$( \frac{x + 3}{ {x}^{2} - 3x } + \frac{12}{9 - {x}^{2} } )\cdot \frac{3x}{x-3} = \frac{3}{x + 3} \\$
$1) \: \frac{x + 3}{ {x}^{2} - 3x} + \frac{12}{9 - {x}^{2} } = \frac{x + 3}{x(x - 3)} - \frac{12}{ {x}^{2} - 9} = \\ = \frac{x + 3}{x(x - 3)} - \frac{12}{ {x}^{2} - {3}^{2} } = \frac{x + 3}{x(x - 3)} - \frac{12}{(x - 3)(x + 3)} = \\ = \frac{(x + 3)^2-12x}{x(x - 3)(x + 3)} = \frac{ {x}^{2} + 2\cdot x\cdot3 + 3^{2} - 12x}{x(x - 3)(x + 3)} =$
$= \frac{ {x}^{2} + 6x + {3}^{2} - 12x }{x(x - 3)(x + 3)} = \frac{ {x}^{2} - 6x + {3}^{2} }{x(x - 3)(x + 3)} = \\ = \frac{ {x}^{2} - 2\cdot x\cdot3 + 3^{2}}{x(x - 3)(x + 3)} = \frac{ {(x - 3)}^{2} }{x(x - 3)(x + 3)} = \frac{ x - 3}{x(x + 3)}$
$2) \: \frac{ x - 3}{x(x + 3)} \cdot \frac{3x}{x - 3} = \frac{3}{x + 3} \\$
Ответ:
$\frac{3}{x +3} \\$

Предыдущий вопрос

Следующий вопрос

Интересные вопросы

Предмет: Русский язык, автор: Аноним

Помогите пожалуйста сделать номер 2

6 лет назад

Предмет: Английский язык, автор: Аноним

Помогите пожалуйста!

6 лет назад

Предмет: География, автор: karinakhazhanets

Что такое лесо?
Помогите срочно

6 лет назад

Предмет: Алгебра, автор: baku2015baku

Пожалуйста помогите умоляю

9 лет назад

Предмет: Биология, автор: Maibah2004

какая ткань отсутствует в организме животного
1) фотосинтезирующая
2)покровная
3)мышечная
4)соединительная

9 лет назад