Предмет: Алгебра,
автор: Лиечка7
Изобразить на координаний плоскости множество точек (x; y), которые
удовлетворяют неравенство:
Приложения:
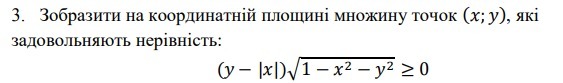
NeZeRAvix:
Очень приятная задача. С построением графиков, надеюсь, у вас проблем не возникнет.
Ответы
Автор ответа:
1
Изобразить на координатной плоскости множество точек (x; y), которые удовлетворяют неравенству (y-|x|)√(1-x²-y²)≥0
Решение:
ОДЗ:
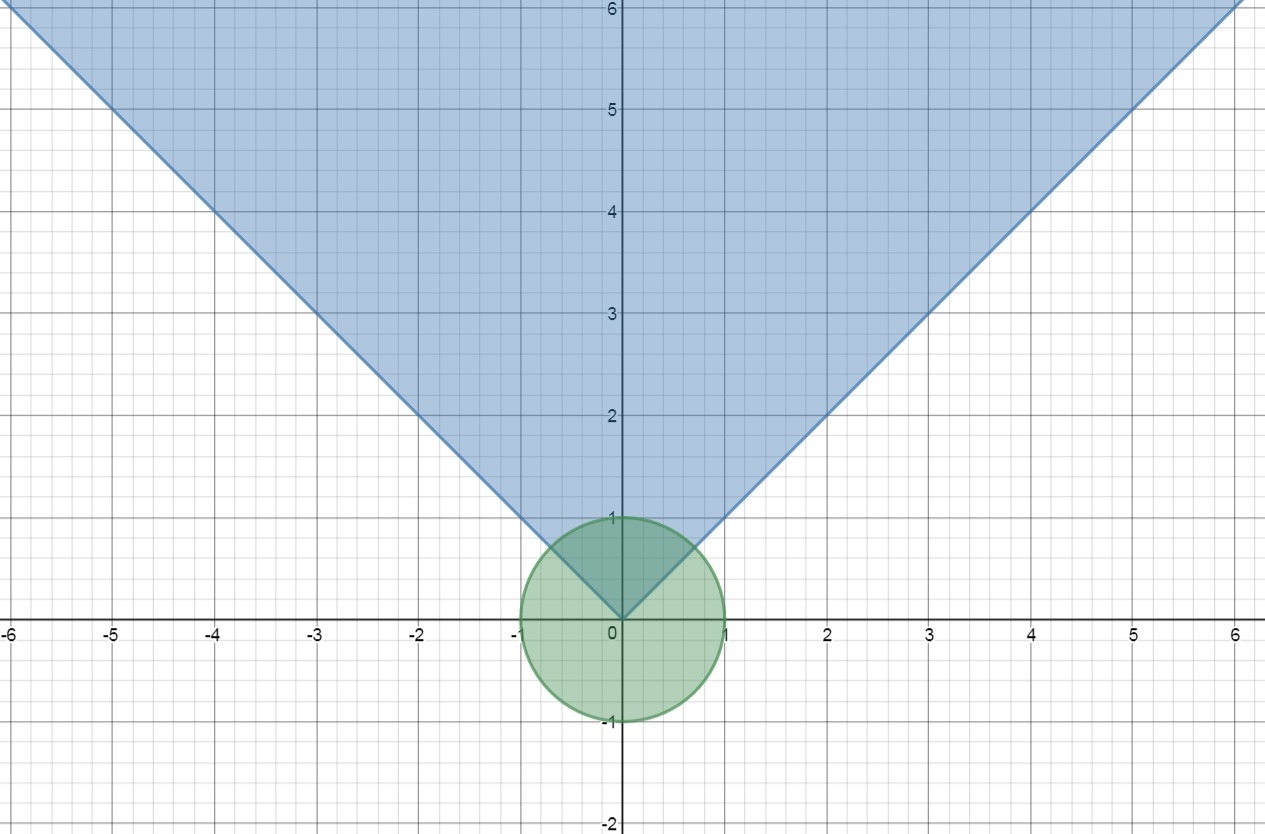
ОДЗ представляет собой множество точек, находящихся внутри окружности с центром (0; 0) и радиусом 1.
Так как √(1-x²-y²)≥0, то для выполнения неравенства требуется
Это "галочка" y=|x|. Решениями является все, что выше нее находится.
Изображение с координатной плоскостью прикреплено. Удовлетворяют неравенству те точки, которые лежат на пересечении синего и зеленого.
Приложения:
Интересные вопросы
Предмет: Физкультура и спорт,
автор: dariaesenbekova
Предмет: Математика,
автор: ratalas96
Предмет: Геометрия,
автор: Tollkris
Предмет: Математика,
автор: ннрп
Предмет: Математика,
автор: sikachevai