Предмет: Геометрия,
автор: Аноним
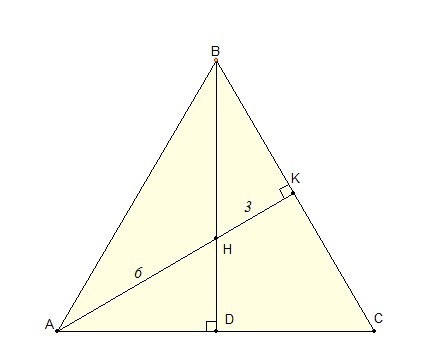
в равнобедренном треугольнике авс (ав=вс) точка h ортоцентр. Высота АК=9 см, а отрезок АН=6 см. Найдите площадь треугольника авс
Ответы
Автор ответа:
0
Поскольку HK=AK-AH=3 и AH:HK=2:1, то AK - медиана (и высота по условию). Тогда треугольник ABC - равносторонний и его площадь равна
где а - сторона. Найдем ее:
Поскольку треугольник равносторонний, то угол AHB = 120 градусов. Тогда по теореме косинусов:
и
Приложения:
Интересные вопросы
Предмет: Русский язык,
автор: prostoezik23
Предмет: Алгебра,
автор: shchepkinaanna34
Предмет: Математика,
автор: sagalovakira2011
Предмет: География,
автор: seny12krapivina
Предмет: Математика,
автор: Изи666