Предмет: Алгебра,
автор: Бальтазар11
Найдешь область определения функции y=⁴√(2-x) (x²-9)
MusikaWinx:
Там под корнем (2-х) или все выражение (2-х)*(x^2 - 9)?
Все выражение
Слушай а можешь помочь с этим, ³√125*216
216 = 6^3, 125 = 5^3. ³√(5^3 * 6^3) = 5*6 = 30.
Ответы
Автор ответа:
2
Нахождение области определения функции в данном случае сводится к решению неравенства. Так как сама функция представляет собой радикал четной степени, то подкоренное выражение должно быть неотрицательным. То есть:
(2-x)*(x^2 - 9) ⩾ 0.
Для удобства заменим (2-х) на (х-2), изменим знак неравенства на противоположный, и разложим x^2 - 9 = (x-3)*(x+3). Получаем:
(x-2)*(x-3)*(x+3) ⩽ 0.
Это неравенство решаем методом интервалов: разбиваем числовую прямую нулями на интервалы и смотрим значение выражения на каждом из них. Выбираем отрицательные и записываем ответ. Решение во вложении.
Ответ: D(y) = (-∞; -3]⋃[2; 3].
Приложения:
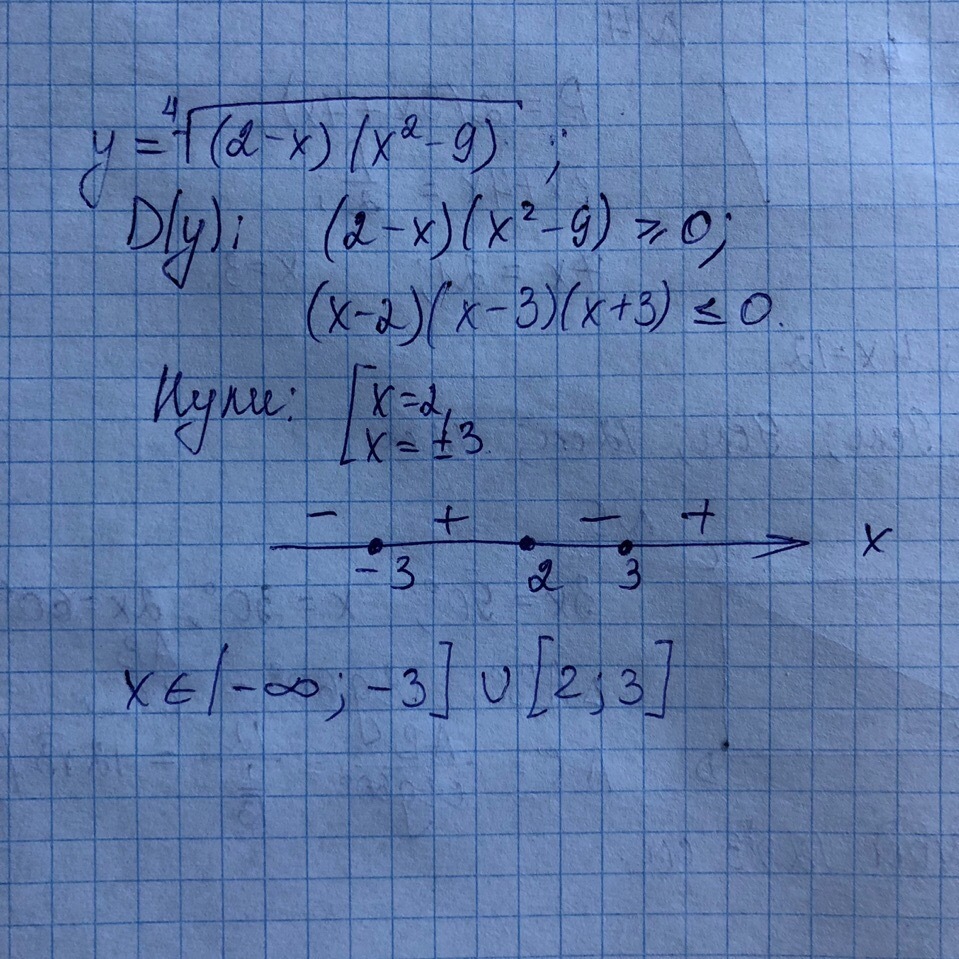
Спасибо тебе огромное за ответ
Интересные вопросы
Предмет: Русский язык,
автор: beldymenkoa
Предмет: История,
автор: sofiaibatullina
Предмет: Алгебра,
автор: arturovaalina9
Предмет: Литература,
автор: Postawnevnikit
Предмет: Математика,
автор: 10Елена10