Предмет: Алгебра, автор: winxclub123

помогите с пределом пожалуйста

Приложения:

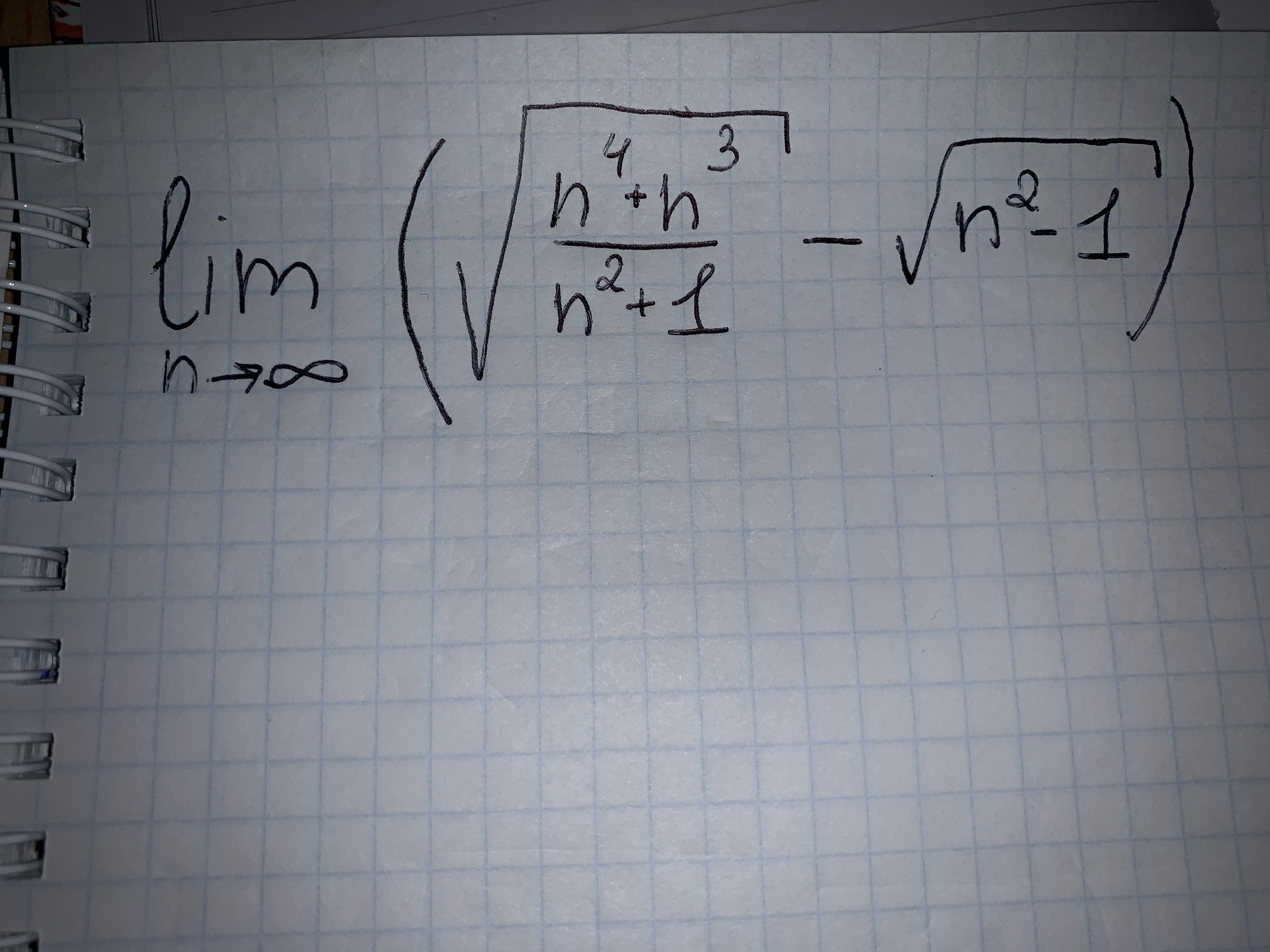
Ответы

Автор ответа: NNNLLL54

$\lim\limits _{n \to \infty}(\sqrt{\frac{n^4+n^3}{n^2+1}}-\sqrt {n^2-1})=\lim\limits _{n \to \infty}\frac{\sqrt{n^4+n^3}-\sqrt{(n^2-1)(n^2+1)}}{\sqrt{n^2+1}}=\\\\=\lim\limits _{n \to \infty}\frac{\sqrt{n^3(n+1)}-\sqrt{(n+1)(n-1)(n^2+1)}}{\sqrt{n^2+1}}=\\\\=\lim\limits _{n \to \infty}\frac{\sqrt{n+1}\cdot (\sqrt{n^3}-\sqrt{(n-1)(n^2+1)})}{\sqrt{n^2+1}}=$

$=\lim\limits _{n \to \infty}\frac{\sqrt{n+1}\cdot (n^3-(n-1)(n^2+1))}{\sqrt{n^2+1}\cdot (\sqrt{n^3}+\sqrt{(n-1)(n^2+1)}}=\lim\limits _{n \to \infty}\frac{\sqrt{n+1}\cdot (n^2-n+1)}{\sqrt{n^2+1}\cdot (\sqrt{n^3}+\sqrt{n^3+n-n^2-1})}=\\\\=\lim\limits _{n \to \infty}\frac{\sqrt{n}\cdot n^2}{\sqrt{n^2}\cdot 2\sqrt{n^3}}=\lim\limits _{n \to \infty}\frac{n^{5/2}}{2n^{5/2}}=\frac{1}{2}$

Предыдущий вопрос

Следующий вопрос

Интересные вопросы

Предмет: Физика, автор: Diretka

хлопчик тягне по снігу санчата, прикладаючи годизонтальну силу 90Н Санчата рухаються рівномірно прямолінійно. визначте коефіцієнт тертя санчат по снігу, якщо сила нормальної реакції опори, що діє на санчата дорівнює 360Н

5 лет назад

Предмет: Математика, автор: asdtuy812010

РЕШИТЬ ЗАДАЧУ С ПОМОЩЬЮ УРАВНЕНИЯ. В магазине"Игрушка",на полке в двух коробках лежали мячи,их было поровну.Из первой коробки купили 10 мячей,из второй коробке продали30 мячей,после чего в первой коробке стало мячей в 2 раза больше.Сколько стало мячей в первой коробке? ПОМОГИТЕ ПОЖАЛУЙСТА У МЕНЯ СОРР

5 лет назад

Предмет: Физкультура и спорт, автор: firrknifekz

сколько килограм или грамм в 2628,8072 джоулей
срочно нужно физрук думает что я списаваю