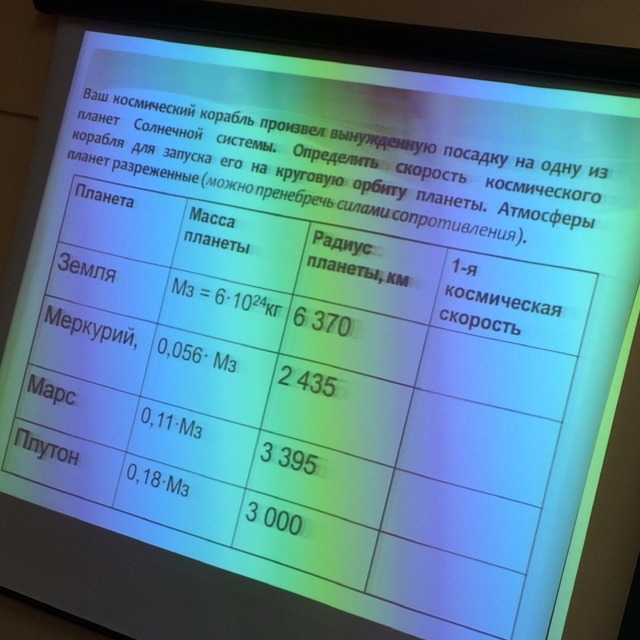
Ваш космический корабль произвел вынужденную посадку на одну из планет Солнечной системы. Определить скорость космического корабля для запуска его на круговую орбиту планеты. Атмосферы планет разреженные (можно пренебречь силами сопротивления). Планета Масса планеты Радиус планеты, км 1-я космическая скорость Земля Мз = 6·1024кг 6 370 Меркурий, 0,056·Мз 2 435 Марс 0,11·Мз 3 395 Плутон 0,18·Мз 3 000

Для движения по круговой орбите необходимо, чтобы действие силы тяготения F1 уравновешивалось действием центробежной силы F2. Пусть m1 и m2 - массы космического корабля и планеты, R - расстояние от космического корабля до центра планеты, v - линейная скорость космического корабля (первая космическая скорость). Так как F1=G*m1*m2/R², а F2=m1*v²/R, то из равенства F1=F2 следует равенство G*m2/R=v², откуда v=√(G*m2/R). Если расстояние от поверхности планеты до космического корабля мало по сравнению с радиусом планеты R1, то можно считать, что R≈R1. Тогда v≈√(G*m2/R1). Подставляя в эту формулу данные из таблицы, находим:

1)  Для Земли: v≈7924,64 ≈7,9 км/с.

2) Для  Меркурия: v≈3033 м/с ≈ 3 км/с.

3) Для Марса: v≈3600 м/с=3,6 км/с.

4) Для Плутона: v≈4900 м/с=4,9 км/с.