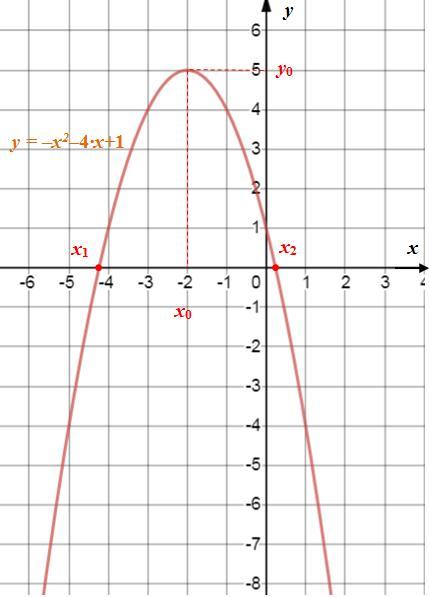
используя результаты вычислений в задании 1а постройте график функции y -x^2-4x+1
Ответы
Ответ:
Дана функция y = -x² - 4·x + 1. Исследуем свойства функции.
1-a) Область определения функции D(y)=R.
Данная функция - эта парабола. Коэффициент при главном члене x² равен -1<0, поэтому ветви параболы направлены вниз.
Находим координаты вершины параболы:
Вершина параболы находится в точке (-2; 5). В силу этого область значений функции E(y)=(-∞; 5].
Находим нули функции:
y = 0 ⇔ -x² - 4·x + 1 = 0 ⇔ x² + 4·x - 1 = 0:
D=4²-4·1·(-1)=16+4=20=(2√5)²,
x₁=(-4-2√5)/(2·1)=-2-√5≈-2-2,2=-4,2,
x₂=(-4+2√5)/(2·1)=-2+√5≈-2+2,2=0,2.
1-б) Зная направление ветвь параболы для построения графика параболы достаточно 3 различных точек: одна из них - вершина параболы и два различных точек. Известны координаты вершины и нули функции. На основе этих значений построим график функции (см. рисунок).