Предмет: Математика,
автор: nbbc
Срочно!
Помогите решить!
В целом знаю как решать ,но хочу светиться;)
Помогите с 1,2,3
Lim x→3 cosx/(3-x)
Lim x→0 tgx-sinx/((x)(1-cosx))
Приложения:
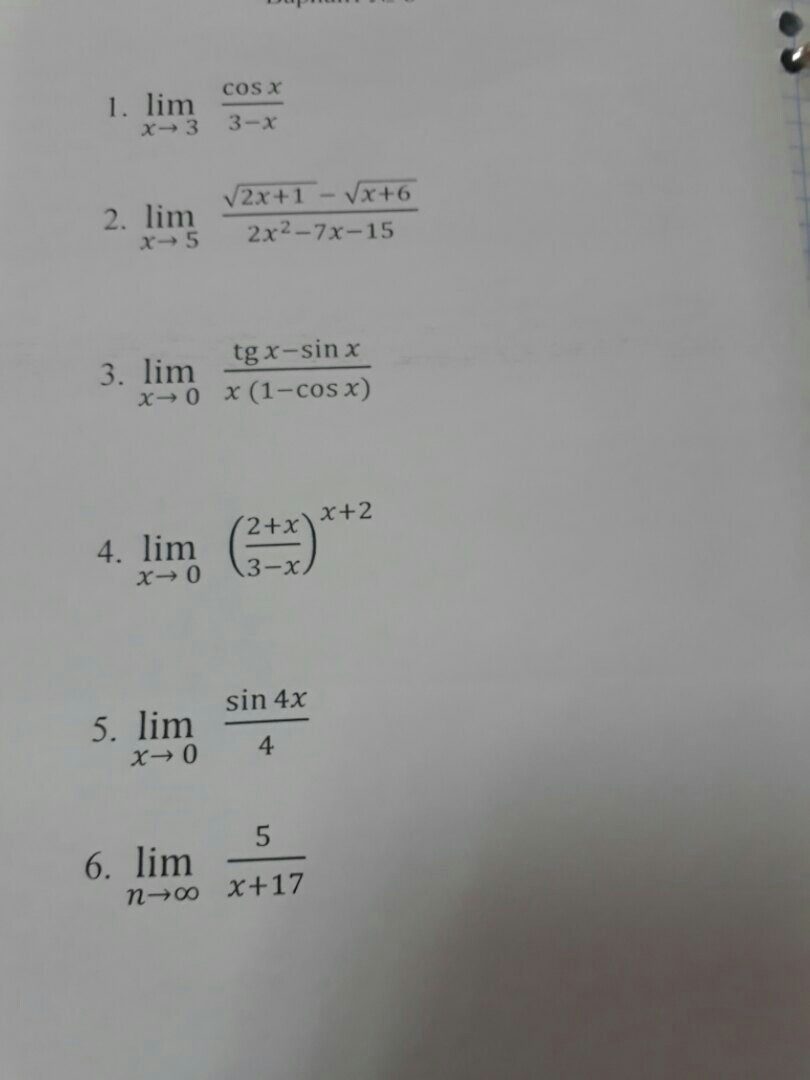
Ответы
Автор ответа:
1
Интересные вопросы
Предмет: Математика,
автор: kvolodin931
Предмет: Математика,
автор: karll50
Предмет: Литература,
автор: alinaberhanova2009
Предмет: Алгебра,
автор: melnich
Предмет: Геометрия,
автор: gora01