Предмет: Математика, автор: Tester16

2.96, помогите разобраться как это решать

Приложения:

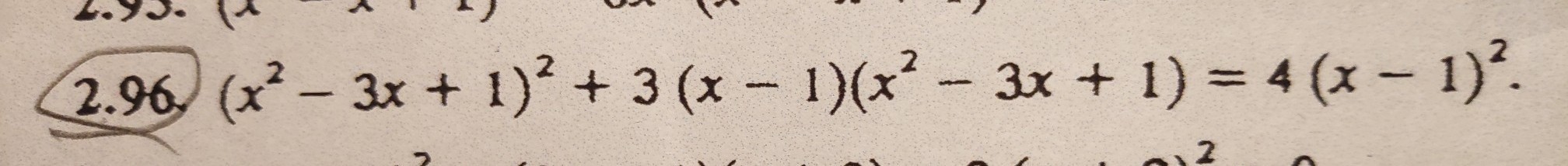
NNNLLL54: как однородное уравнение: разделить на (х-1)^2 .

Tester16: а дальше как?

Tester16: ауу

Tester16: спасибо

Ответы

Автор ответа: NNNLLL54

1

$(x^2-3x+1)^2+3(x-1)(x^2-3x+1)=4(x-1)^2\; |:(x-1)^2\ne0\; \; \to \; \; x\ne 1\\\\(\frac{x^2-3x+1}{x-1})^2+3\cdot \frac{x^2-3x+1}{x-1}-4=0\; ,\; \; \; t=\frac{x^2-3x+1}{x-1}\\\\t^2-3t-4=0\; ,\; \; t_1=-1\; ,\; \; t_2=4\; \; (teorema\; Vieta)\\\\a)\; \; \frac{x^2-3x+1}{x-1}=-1\; \; ,\; \; x^2-3x+1=-x+1\; ,\; \; x^2-2x=0\; ,\; x(x-2)=0\; ,\\\\x_1=0\; ,\; \; x_2=2\\\\b)\; \; \frac{x^2-3x+1}{x-1}=4\; ,\; \; x^2-3x+1=4x-4\; ,\; \; x^2-7x+5=0\; ,\\\\x_1=\frac{7-\sqrt{29}}{2}\; ,\; \; x_2=\frac{7+\sqrt{29}}{2}\; .$

$Otvet:\; \; x=0\; ,\; x=2\; ,\; x=\frac{7-\sqrt{29}}{2}\; ,\; \; x=\frac{7+\sqrt{29}}{2}\; .$

Предыдущий вопрос

Следующий вопрос

Интересные вопросы

Предмет: Қазақ тiлi, автор: dilnazmuratkyzy96

6. Бір ұлттық ойын туралы мәлімет жазып, ойнау әдісін түсіндірін- дер. Баланың өсуіне тигізетін пайдасына тоқталыңдар.

5 лет назад

Предмет: История, автор: elvira100000

Объясните значение слова налог в истории

5 лет назад

Предмет: Геометрия, автор: kurlenkova35

ПОМОГИТЕ ПОЖАЛУЙСТА!!!!!!

5 лет назад

Предмет: Математика, автор: лог9

пж
пж помогите очень прошу

9 лет назад

Предмет: Химия, автор: капусточка1

цукроза-глюкоза-етанол-натрій етилат

9 лет назад