Предмет: Геометрия, автор: Novaya22

100 баллов!
В правильной треугольной пирамиде апофема создает с её высотой угол Альфа. Если отрезок, которые соединяет основание высоты с серединой апофемы равно а, то чему равна площадь основания пирамиды? Решение обязательно с рисунком.

Ответы

Автор ответа: Mihail001192

В правильной треугольной пирамиде апофема создает с её высотой угол Альфа. Если отрезок, которые соединяет основание высоты с серединой апофемы равно а, то чему равна площадь основания пирамиды?

РЕШЕНИЕ:

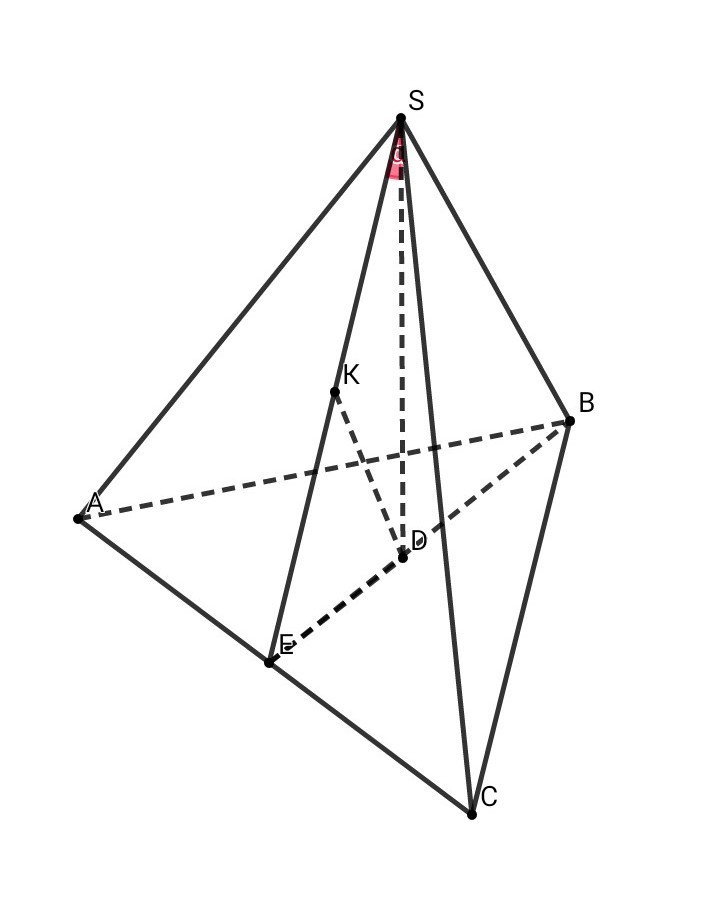
• Рассмотрим тр. SED (угол SDE = 90°):
В прямоугольном треугольнике медиана, проведённая из вершины прямого угла к гипотенузе, равна её половине =>
SE = 2 • KD = 2a
sin@ = ED / SE => ED = sin@ • SE = 2a•sin@
• Рассмотрим тр. АВС ( равносторонний ):
BE = 3 • ED = 3 • 2a•sin@ = 6a•sin@
АС = 2V3ВЕ / 3 = 2V3 • 6a•sin@ / 3 = 4V3asin@

S abc = AC^2 • V3 / 4 = ( 4V3asin@ )^2 • V3 / 4 = 16 • 3 • a^2 • ( sin@ )^2 • V3 / 4 = 12V3•a^2•(sin@)^2

ОТВЕТ: 12V3•a^2•(sin@)^2

Приложения:

Novaya22: за каким свойством ВЕ=3ЕД?

Mihail001192: тр. АВС - равносторонний, поэтому высоты, медианы и биссектрисы будут совпадать. Медианы треугольника пересекаются в отношении 2 : 1 , считая от вершины. ВD : DE = 2 : 1 , DE = ( 1/3 ) • BE , BE = 3•DE.

Novaya22: поняла. спасибо.

Novaya22: За каким свойством нашли АС?

Mihail001192: Остальные формулы, которые приведены в решении, выводятся из элементов равносторонннего треугольника, для упрощения действий. Например, зная высоту, как найти сторону; зная радиус, как найти высоту и т.д.

Mihail001192: Их несложно вывести: ВС = 2а , СЕ = а , по теореме Пифагора , ВЕ = h = аV3 / 2 , a = 2V3•h / 3

Novaya22: Попробуйте решить другие мои задачи