Предмет: Геометрия,
автор: osbzt
В трапеции ABCD боковая сторона АВ равна диагонали BD. Точка М - середина диагонали АС. Прямая ВМ пересекает отрезок СD в точке Е. Докажите, что ВЕ=СЕ
Ответы
Автор ответа:
4
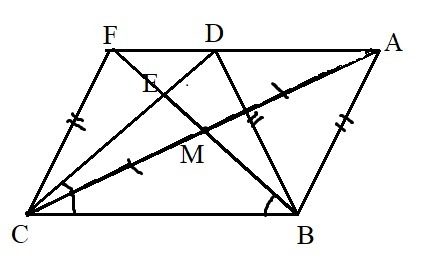
Проведём CF || AB, F ∈ AD. AF || BC, т. к. AD || BC как основания трапеции, CF || AB по построению ⇒ ABCF - параллелограмм ⇒ AB = CF. Но AB = BD по условию, значит, BD = CF ⇒ BDFC - равнобедренная трапеция.
Так как M - середина диагонали AC параллелограмма ABCF ⇒ M ∈ BF. Тогда BF и CD - диагонали равнобедренной трапеции. Они образуют с основаниями равные углы, отсюда треугольник BEC - равнобедренный ⇒ BE = CE, что и требовалось доказать.
Приложения:
Интересные вопросы
Предмет: Английский язык,
автор: Fox118711
Предмет: Математика,
автор: sonia0908
Предмет: Геометрия,
автор: el968714
Предмет: Обществознание,
автор: dmitryyy1
Предмет: Математика,
автор: nesty1984