Предмет: Геометрия,
автор: plague21
ПОМОГИТЕ ПОЖАЛУЙСТА РЕШИТЬ!! ТЕМА КОНУСЫ!!!
ПЛОСКОСТЬ ПРОХОДИТ ЧЕРЕЗ ВЕРШИНУ КОНУСА И ПЕРЕСЕКАЕТ ЕГО ОСНОВАНИЕ.НАЙДИТЕ ПЛОЩАДЬ ПОЛУЧЕННОГО СЕЧЕНИЯ, ЕСЛИ РАДИУС КОНУСА РАВЕН 3 КОРЕНЬ ИЗ 2, ОБРАЗУЮЩАЯ РАВНА КОРЕНЬ ИЗ 34, А ПЛОСКОСТЬ СЕЧЕНИЯ ОБРАЗУЕТ УГОЛ 45 ГРАДУСОВ С ВЫСОТОЙ КОНУСА.
Приложения:

Ответы
Автор ответа:
2
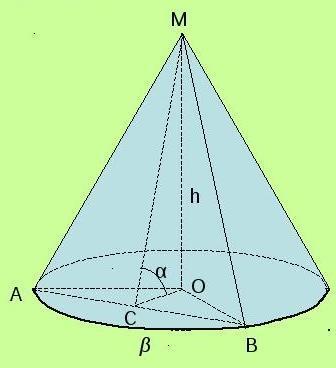
смотри на чертеже
OB=3√2 радиус основания
MB=34 образующая конуса
площадь сечения равна площади треугольника AMB: S=AB*MC/2
ΔOMB - прямоугольный, OM=√(MB²-OB²)=√(34-18)=√16=4
ΔOMC - прямоугольный, ∠α=45° ⇒OM=ОС MC=√(OM²+OC²)=√(16+16)=4√2
ΔOBC - прямоугольный ⇒ВС=√(OB²-OC²)=√(18-16)=√2
AB=2BC=2√2
S=2√2*4√2/2=8
Приложения:
plague21:
большое спасибо
Интересные вопросы
Предмет: Математика,
автор: dgarackun
Предмет: Алгебра,
автор: artempyalisov
Предмет: Математика,
автор: kamilladolgunova
Предмет: Физика,
автор: chuchman1976chuchman
Предмет: Алгебра,
автор: serhfedorov76