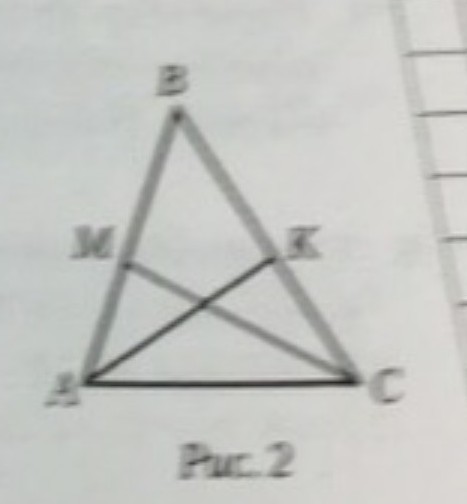
В равнобедренном треугольникн ABC с основанием AC проведены биссектрисы AK и CM. Докажите, что BK=BM

Ответ:

∠ВАК = 1/2 ∠ВАС, так как АК биссектриса ∠ВАС,

∠ВСМ = 1/2 ∠ВСА, так как СМ биссектриса ∠ВСА,

∠ВСА = ∠ВАС как углы при основании равнобедренного треугольника, значит и

∠ВАК = ∠ВСМ.

В треугольниках ВАК и ВСМ:

АВ = СВ как боковые стороны равнобедренного треугольника,

∠ВАК = ∠ВСМ, как доказано выше,

∠В - общий, следовательно

ΔВАК = ΔВСМ по стороне и двум прилежащим к ней углам.

В равных треугольниках напротив равных углов лежат равные стороны, значит ВК = ВМ.