Предмет: Математика,
автор: varvara207i
Окрашенный куб распилили на 27 одинаковых кубиков с ребром 1 см ( рис.110) .У скольких маленьких кубиков окрашена только одна грань;только две грани;три
Ответы
Автор ответа:
9
Ответы по тексту решения.
Пошаговое объяснение:
Рисунок к задаче в приложении.
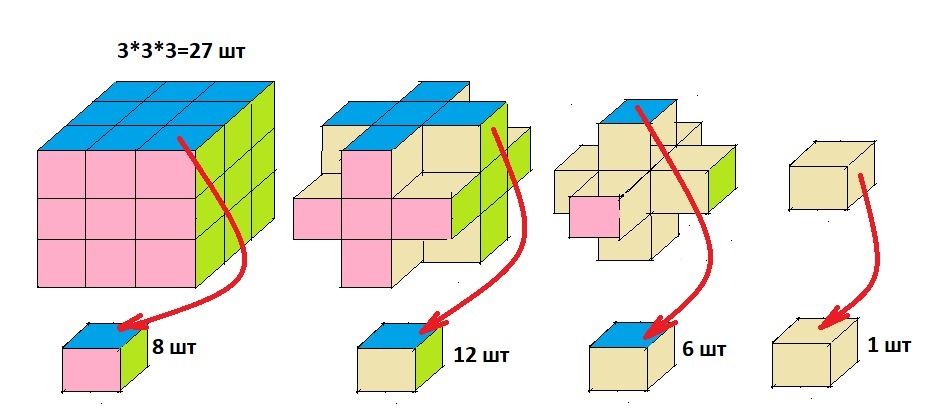
Всего кубиков - 27.
Ребро куба - n =∛27 = 3 шт.
Покрашены с трёх сторон - в вершинах куба.
N3 = 8 шт - с трёх сторон - ОТВЕТ - не зависит от размера кубика.
Покрашены с двух сторон - на 12-ти рёбрах, кроме кроме двух углов.
N2 = 12*(n-2) = 12*1 = 12 шт - с двух сторон - ОТВЕТ
С одной стороны покрашены в центре грани.
N1 = 6*(n-2) = 6 шт - с одной стороны - ОТВЕТ
И, дополнительно, остался в центре кубика.
N0 = (n-2)³ = 1 - не окрашен.
Проверка: 8 + 12 + 6 + 1 = 27 - правильно.
Приложения:
love67:
шикарно
Интересные вопросы
Предмет: Английский язык,
автор: pavlova66m41
Предмет: Физика,
автор: sergeykaportsev3
Предмет: География,
автор: namagoytivan
Предмет: Обществознание,
автор: yanochkamelnichenko
Предмет: Химия,
автор: Аноним