Предмет: Геометрия,
автор: Exotica99
Основание пирамиды SABCD — параллелограмм ABCD с центром
O. Точка M — середина отрезка AO.
Постройте сечение пирамиды плоскостью, проходящей через
точку M параллельно прямым SA и BD
Ответы
Автор ответа:
9
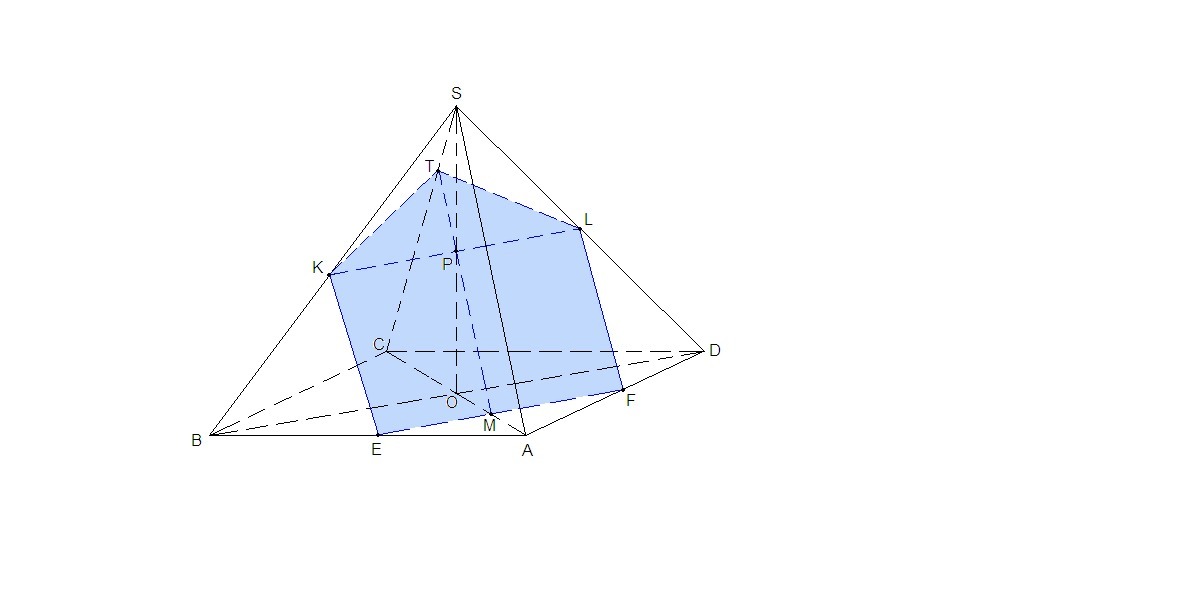
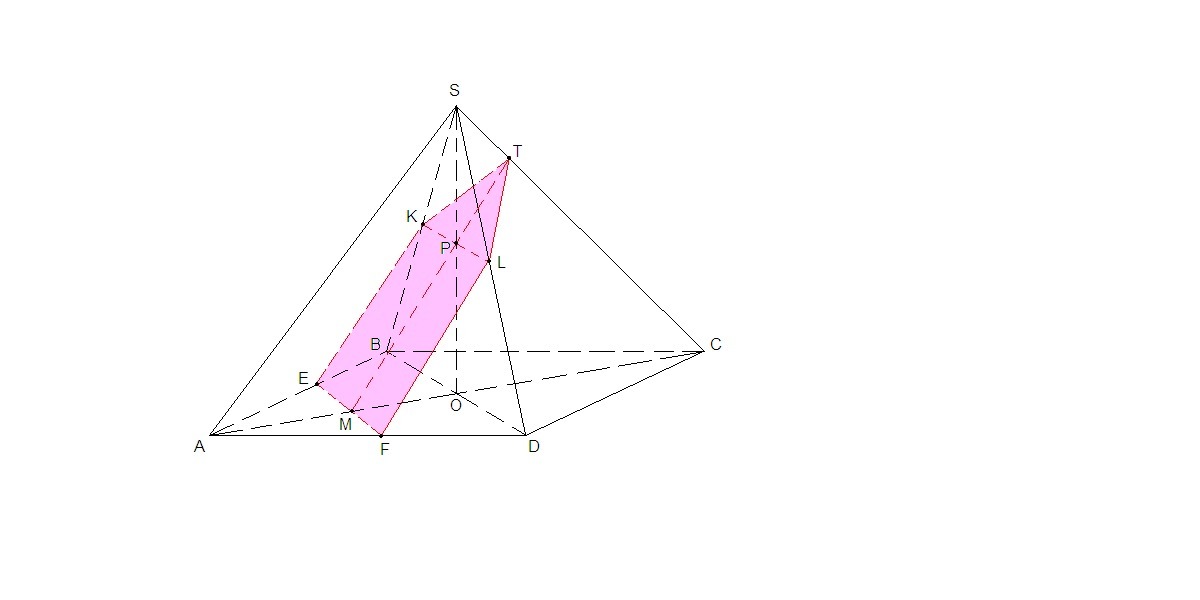
Через точку М в основании ABCD проведем прямую, параллельную BD. Точки пересечения этой прямой с АВ и AD соответственно Е и F.
В плоскости SAB проведем ЕК║SA, а в плоскости SAD прямую FL║SA.
Соединим точки К и L.
Прямая KL лежит в плоскости BSD, значит она пересечет отрезок, соединяющий вершину пирамиды с точкой О - SO. Р - точка пересечения.
Точки М и Р лежат в плоскости ASC. Проведем прямую МР. Она пересечет ребро SC в точке Т.
EFLTK - искомое сечение.
Доказательство:
Так как EF║BD, то плоскость сечения параллельна прямой BD.
Так как ЕК║SA, то плоскость сечения параллельна прямой SA.
Приложения:
Интересные вопросы
Предмет: Информатика,
автор: jkortv
Предмет: Математика,
автор: kvasninaevgenia13
Предмет: Математика,
автор: jgbvf
Предмет: Математика,
автор: ghoralskaia88