Предмет: Алгебра, автор: Sola17

почему промежуток (-2;0);(0;2) входит?

Приложения:

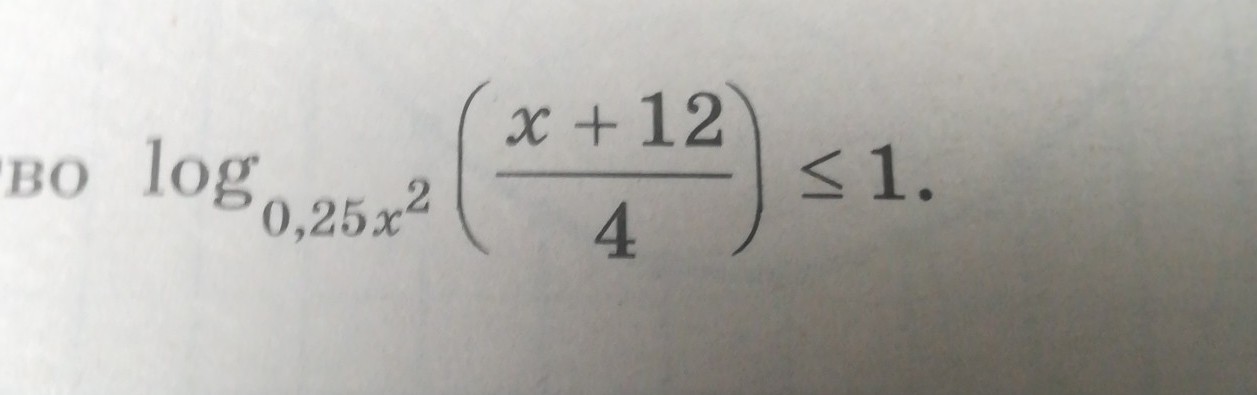
Ответы

Автор ответа: tane4ka2771

Сначала определим допустимые значения переменной:

$\left \{ {{x+12>0} \atop {x\neq =±2;0}\} \right.$

[/tex]㏒ $(\frac{x+12}{4} )\leq1$

x∈(-12;-2)(2;∞) функция y=㏒ₐx $\frac{x+12}{4} \leq 0,25x^{2}$

$x^{2} -x-12\geq 0$

$x^{2} -x-12=0; D=1+48=49$

x= $\frac{1-7}{2} =-3$ ; x= $\frac{1+7}{2} =4$

x∈(-∞;-3)(4;∞). Учитывая ОДЗ x∈(-12;-3)(4;∞).

Пусть x∈(-2;0)(0;2). При эти значениях x функция убывающая. Значит

$\frac{x+12}{4} \geq0,25x^{2}$

x+12 $\geq x^{2}$

$x^{2} -x-12\leq 0$ .

x∈(-3;4 ). Учитывая ОДЗ x∈(-2;0)(0;2)

Ответ: x∈(-12;-3)(-2;0)(0;2)(4;∞).

Sola17: почему при этих значениях функция убывающая? с чего мы это взяли?

tane4ka2771: возьмите значение х из промежутка, например -1 или 1. Умножте на 0,25. получим основание логарифма меньше 1. то есть функция убывающая

Sola17: ааа, всё спасибо

tane4ka2771: конечно лучше решить квадратное неравенство. когда основание меньше 1, когда больше 1. Но тут не очень хороший редактор формул. да и неудобно чертить решение квадратного неравенства

maksimcat: -3 и 4 входят в ответ; скобки квадратные должны быть

Автор ответа: maksimcat

ответ на фото//////////////////

Приложения: