Предмет: Математика,
автор: Тuтан
Найти асимптоты графика функции y=(21-x²)/(7x+9).
Я знаю, что уравнение асимптоты – y=kx+b, где k=lim[x→∞](f(x)/x), b=lim[x→∞](f(x)-kx). У меня получилось, что b=∞, получается, что наклонной асимптоты не существует, но y=(21-x²)/(7x+9) – это гипербола, разве у неё может не быть наклонной асимптоты?
Ответы
Автор ответа:
0
Пошаговое объяснение:
Вертикальная асимптота: х = - 9/7 - ответ
Находим значение k для наклонной асимптоты
k = lim(+oo) (21-x²)/(7x²+9x) = - 1/7. (разделили на х²). Находим сдвиг b.
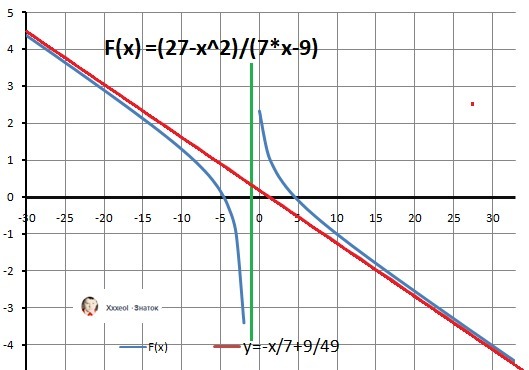
Наклонная асимптота: Y = x/7 + 9/49 - ответ
Всё прекрасно получилось.
График функции в приложении - подарок.
Приложения:
xxxeol:
Опечаточки. b = +9/49
Отстаешь. Уже исправлено.
Приглашай в друзья. Обожаю строить графики.
Можно будет писать сообщения и ответы - "без очереди".
У нас же дробь была в примере и всё сократилось. Была неопределённость оо/оо.
Интересные вопросы
Предмет: Математика,
автор: nloseva1505
Предмет: Английский язык,
автор: popova221257
Предмет: Английский язык,
автор: Aleksandra19000
Предмет: Математика,
автор: tank5553Scooby
Предмет: Геометрия,
автор: bashmakovaenot