Помогите с алгеброй! Даю 100 баллов..
нужно Решить систему уравнений: 1 методом Крамера; 2) средствами матричного исчисления ; 3) методом Гаусса. вычисления проводить с обычными дробями, не используя десятичных приближений
первым етодом пробовала, определитель получила равный нулю... а дальше не понимаю!
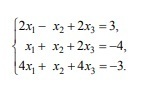

Ответы
Решить следующую систему линейных уравнений методом Крамера:
2 ·x1
+
0 ·x2
+
0 ·x3
=
3
0 ·x1
+
0 ·x2
+
2 ·x3
=
−4
4 ·x1
+
0 ·x2
+
4 ·x3
=
−3
Запишем ее в матричной форме: Ax=b, где
A=
2
0
0
0
0
2
4
0
4
, b=
3
−4
−3
Шаг 0:
Найдем определитель матрицы A:
A=
2
0
0
0
0
2
4
0
4
Для вычисления определителя матрицы, приведем матрицу к верхнему треугольному виду.
Выбираем самый большой по модулю ведущий элемент столбца 1. Для этого меняем местами строки 1 и 3. При этом меняется знак определителя на "-".
4
0
4
0
0
2
2
0
0
Исключим элементы 1-го столбца матрицы ниже главной диагонали. Для этого сложим строку 3 со строкой 1, умноженной на -2/4:
4
0
4
0
0
2
0
0
−2
Невозможно выбрать ненулевой ведущий элемент на столбце 2. Следовательно определитель матрицы A равен нулю: Δ==0.