Предмет: Математика, автор: Nastya171167

нужно найти производные функций

Приложения:

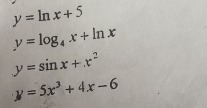
Ответы

Автор ответа: rina2403k

0

$y = ln(x) + 5 \\ \frac{d}{dx} ( ln(x) + 5) \\ \frac{d}{dx} ( ln(x) ) + \frac{d}{dx} (5) \\ \frac{1}{x} + 0 = \frac{1}{x} \\ y = log_{4}(x) + ln(x) \\ \frac{d}{dx} ( log_{2 {}^{2} }(x) + ln(x) ) \\ \frac{d}{dx} ( \frac{1}{2} \times log_{2}(x) + ln(x) ) \\ \frac{d}{dx} ( \frac{1}{2} \times log_{2}(x) ) + \frac{d}{dx} ( ln(x) ) \\ \frac{1}{2} \times \frac{1}{ ln(2)x } + \frac{1}{x} \\ \frac{1 + 2 ln(2) }{2 ln(2)x } \\ y = \sin(x) + x {}^{2} \\ \frac{d}{dx} ( \sin(x) ) + \frac{d}{dx} (x {}^{2} ) \\ \cos(x) + 2x \\ y = 5x {}^{3} + 4x - 6 \\ \frac{d}{dx} (5x {}^{3} ) + \frac{d}{dx} (4 x) - \frac{d}{dx} (6) \\ 5 \times 3x {}^{2} + 4 - 0 \\ 15x {}^{2} + 4$

Автор ответа: IrkaShevko

1

Ответ:

Пошаговое объяснение:

$y' = \frac{1}{x} +0=\frac{1}{x} \\\\y'=\frac{1}{xln4} +\frac{1}{xy} \\\\y'=cosx+2x\\\\y'=15x^2+4$

Формулы:

$(x^n)'=nx^{n-1}\\\\(lnx)'=\frac{1}{x} \\\\(log_ax)'=\frac{1}{xlna} \\\\(sinx)'=cosx$

Предыдущий вопрос

Следующий вопрос

Интересные вопросы

Предмет: Алгебра, автор: eyyryryrye

СРОЧНО!!!!!!Помогите пожалуйста даю 50баллов

Сложи почленно неравенства 13 < 23 и - 0,9 > -3,2.

Ответ:

5 лет назад

Предмет: Русский язык, автор: dfghjkqs

напишите пожалуйста все, что знаете о спряжениях, исключения там, ещё что то

5 лет назад

Предмет: Химия, автор: Тупой321

етен→ етанол→ етилпентаноат →пентанова кислота→ натрій пентаноат
составьте плиз

5 лет назад

Предмет: Математика, автор: ildarlg1

в корзине лежат 13 яблок. С помощью весов можно узнать общий вес любых двух яблок. Как выяснить общий вес всех яблок за 8 взвешиваний?

9 лет назад

Предмет: Математика, автор: чебурек2028

скорость пешехода x км/ч,а велосипедиста y км/ч запишите в виде выражения:

а)скорость удаления при движении в разные стороны.

б)скорость сближения при условии,что велосипедист догоняет пешехода

г)скорость удаления при условии,что велосипедист обогнал пешехода

9 лет назад