Предмет: Геометрия, автор: ursadota

Помогите решить 3 задачи пожалуйста
Признаки подобия треугольников
Найти x и y

Приложения:

Ответы

Автор ответа: teledima00

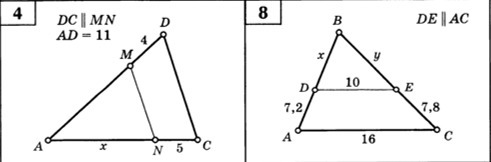
4. Рассмотрим треугольники AMN и ADC

MN ║DC - по условию ⇒ ∠AMN = ∠ ADC и ∠ANM = ∠ACD как соответственные углы при MN ║DC и секущих AD и AC соответственно.

Следовательно, ΔAMN и ΔADC подобны по двум равным углам.

Так как треугольники подобны, то справедливо следующее:

$\displaystyle \frac{AN}{AC} = \frac{AM}{AD}$

AN = x

AC = AN + NC = x + 5

AM = AD - MD = 11 - 4 = 7

AD = 11

$\displaystyle \frac{x}{x+5} = \frac{7}{11} \\ \\ 11x = 7(x+5) \\ \\ 11x = 7x + 35 \\ \\ 4x = 35 \\ \\ \bold{x = \frac{35}{4} = 8\frac 3 4 = 8.75}$

8. Рассмотрим треугольники DBE и ABC

DE║AC - по условию

∠EDB = ∠CAB - соответственные углы при DE║AC и секущей AB

∠B - общий угол

Следовательно, ΔDBE подобен ΔABC под двум равным углам:

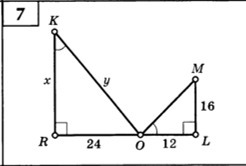
$\begin{array}{lcl} \dfrac{DB}{AB} = \dfrac{DE}{AC} && \dfrac{EB}{CB} = \dfrac{DE}{AC} \\ \\ DB = x && EB = y \\ \\ AB = AD+DB = 7.2+x && CB = CE+EB = 7.8 + y \\ \\\dfrac{x}{7.2+x} = \dfrac{10}{16} && \dfrac{y}{7.8+y}=\dfrac{10}{16} \\ \\ \dfrac{x}{7.2+x} = \dfrac{5}{8} && \dfrac{y}{7.8+y} = \dfrac{5}{8} \\ \\ 8x = 5(7.2+x) && 8y = 5(7.8+y)\\ \\8x = 36+5x && 8y= 39+5y\\ \\3x = 36 && 3y = 39\\ \\\bold{x = 12}&&\bold{y =13}\end{array}$

7. Рассмотрим треугольники RKO и LOM

∠R = ∠L = 90°

∠RKO = ∠LOM

Следовательно, ΔRKO и ΔLOM подобны:

$\dfrac{RK}{OL}=\dfrac{RO}{ML} \\ \\ RK = x, ~OL=12, ~RO = 24, ~ML=16 \\ \\ \dfrac{x}{12} = \dfrac{24}{16} \\ \\\dfrac{x}{12} = \dfrac{3}{2} \\ \\ \bold{x = \dfrac{12\cdot 3}{2} = 18}$