Предмет: Математика, автор: izabella9

.Помогите решить интегралы..

Приложения:
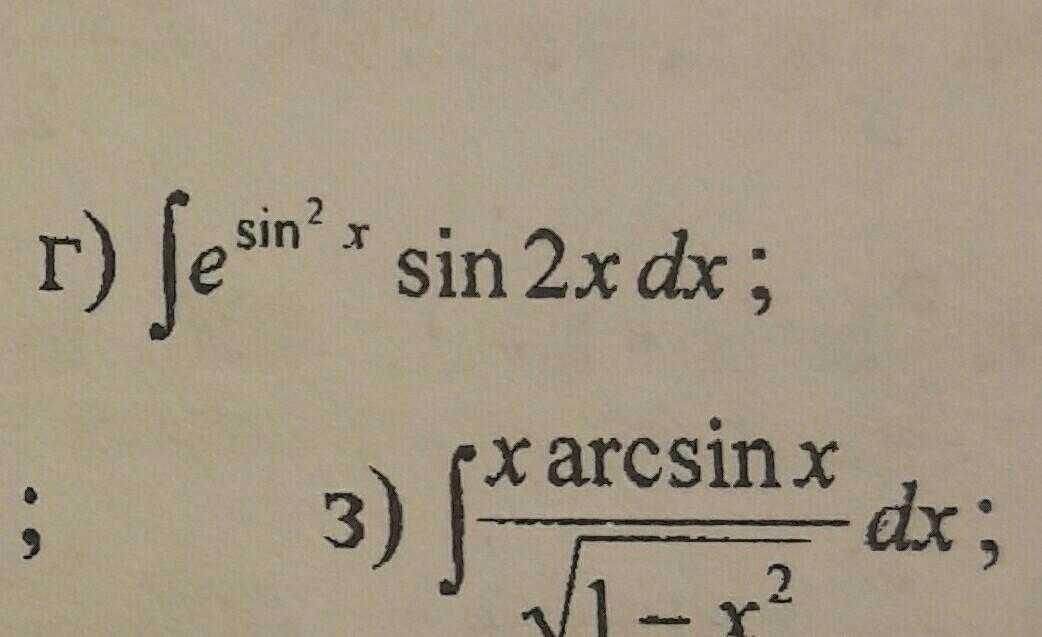
viva34: Оба или только г?
izabella9: оба

Ответы

Автор ответа: Minsk00
1

Ответ:

\int\limits{e^{sin^2x}sin2x \, dx=e^{sin^2x}+C

\int\limits{\frac{x\cdot arcsinx}{\sqrt{1-x^2} }} \, dx =x-\sqrt{1-x^2}\cdot arcsinx+C

Пошаговое объяснение:

\int\limits{e^{sin^2x}sin2x \, dx=\int\limits{e^{sin^2x}\cdot2sinx\cdot cosx \, dx=\begin{vmatrix}t=sin^2x \\ dt=2sinx\cdot cosxdx\end{vmatrix}=

=\int\limits{e^t} \, dt=e^t+C=e^{sin^2x}+C

\int\limits{\frac{x\cdot arcsinx}{\sqrt{1-x^2} }} \, dx

Интегрируем по частям

\int\limits{u} \, dv=u\cdot v-\int\limits {v} \, du

u=arcsinx \; \; \; \; \;du=\frac{1}{\sqrt{1-x^2}}dx

dv=\frac{x}{\sqrt{1-x^2} }dx \; \; \;v=\int\limits{\frac{x}{\sqrt{1-x^2} } } \, dx=\begin{vmatrix}t=x^2\\dt=2xdx\end{vmatrix}=\frac{1}{2} \int\limits{\frac{1}{\sqrt{1-t} } } \, dt=

=-\frac{1}{2} \int\limits{(1-t)^{-\frac{1}{2} }} \,d(1-t)=-\frac{1}{2}\cdot 2(1-t)^{\frac{1}{2} }=-\sqrt{1-t}=-\sqrt{1-x^2}

Подставляем в формулу интегрирования по частям

\int\limits{\frac{x\cdot arcsinx}{\sqrt{1-x^2} }} \, dx=-\sqrt{1-x^2}\cdot arcsinx-\int\limits{-\sqrt{1-x^2}\cdot \frac{1}{\sqrt{1-x^2} } } \, dx=

-\sqrt{1-x^2}\cdot arcsinx+\int\limits{} \, dx=x-\sqrt{1-x^2}\cdot arcsinx+C

izabella9: спасибо
izabella9: есть ВК?
Предыдущий вопрос
Следующий вопрос
Интересные вопросы
Предмет: География, автор: eldanamalik593
Табиғи ресурстар дегеніміз не?? срочна!!!​
5 лет назад
Предмет: Русский язык, автор: melehovlev0
Выполните морфологический разбор причастия и деепричастия Тема шёл по дорожкам сада, вдыхая в себя свежесть начинающегося летнего утра.
5 лет назад
Предмет: Математика, автор: raichel31
4 вариант
1. Дано множество C=5, 6, 7, 8, 9, 10) Составьте множество Д состоящее из трех
элементов, если известно что Сc Д.
5 лет назад
Предмет: Математика, автор: Superstar0
Помогите пожалуйста,срочно надо!
9 лет назад
Предмет: Алгебра, автор: lyazka29
Людииии срочно!!! Задание 91, только 6 пример!!! Плииииз!!!
9 лет назад