Предмет: Математика, автор: dmitriykirillov1997

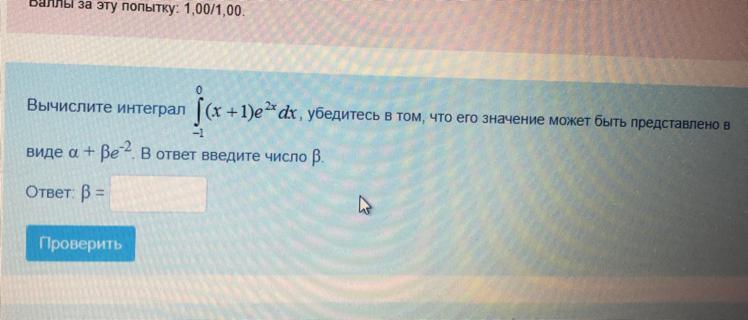
Помогите вычислить интеграл

Приложения:

Ответы

Автор ответа: Аноним

берем интеграл по частям:

Делаем замену

$u=x+1; \ du=dx \\ dv=e^{2x}dx; \ \ v=\frac{1}{2} e^{2x}$

И пользуемся формулой

$\int udv=uv-\int vdu$

$\int\limits^0_{-1} {(x+1)e^{2x}} \, dx =\frac{(x+1)e^{2x}}{2} |^{ \ \ 0}_{-1} \ -\int\limits^0_{-1} {\frac{1}{2} e^{2x}} \, dx=(\frac{(x+1)e^{2x}}{2}-\frac{1}{4} e^{2x}) \ |^0_{-1}= \\ \\ =\frac{1}{2} -\frac{1}{4} +\frac{1}{4} e^{-2}=\frac{1}{4} +\frac{1}{4} e^{-2} \\ \\ OTBET: \ \beta =0.25$

Предыдущий вопрос

Следующий вопрос

Интересные вопросы

Предмет: География, автор: 009viktoria009

Встановіть відповідність між тепловими поясами та їх характеристикою

Назва теплового поясу
Жаркий тепловий пояс

Помірний тепловий пояс

Холодний тепловий пояс

Характеристика
Влітку - полярний день, взимку - полярна ніч.

Пояс має чіткі пори року: зима, весна, літо, осінь. Висота сонця змінюється протягом року.

Пояс отримує велику кількість сонячного тепла протягом року. Сонце двічі на рік буває в зеніті.

5 лет назад

Предмет: Алгебра, автор: illadaskel79

розвяжіть треба вже даю 40 балов!!!!!!!!!

5 лет назад

Предмет: Українська мова, автор: sofa120318

3. Позначте відносний прикметник: а) темний; б) чорний; в) гарячий; г) нічний. 3

5 лет назад

Предмет: Литература, автор: Катянизкина11