помогите пожалуйста, срочно)!

Ответ:

1) 2 см.

2) МА и СВ -перпендикулярные скрещивающиеся прямые, т.к. угол между ними 90°, но лежат они в разных плоскостях.

3) arcsin√(3/5)

4)  РКN ║ ABC

Пошаговое объяснение:

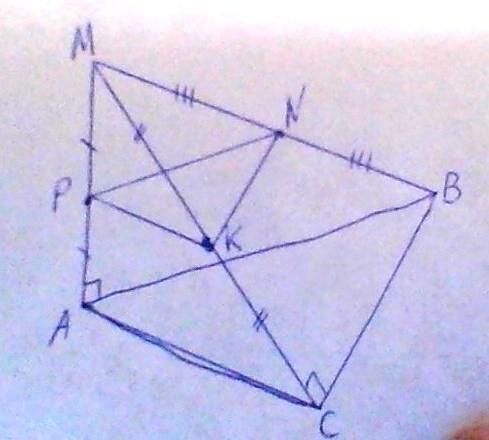
Рассмотрим рисунок.

Найдем катет в прямоугольном равнобедренном ΔАВС. Т.к. он равнобедренный, то АС=ВС=АВ/√2=1.

Рассмотрим ΔМАС. Он прямоугольный с гипотенузой МС и известными нам катетами МА=√3 и АС=1. Найдем МС=√(3+1)=2. МС является расстоянием от т.М до ВС, т.к. МС находится в плоскости ΔАМС и МС⊥ВС.

Рассмотрим  ΔМАВ. Он прямоугольный с гипотенузой МВ, с известными катетами МА и АВ. Найдем МВ=√(2+3)=√5. Угол между МВ и ΔАВС равен ∠АВМ треугольника МАВ. Найдем ∠АВМ=arcsin(МА/МВ)=arcsin√(3/5)

Плоскости РКN ║ ABC, т.к. образованы подобными треугольниками

попарно: МАС и МРК, МСВ и МКN, МАВ и МРN. Подобны они, т.к. у них одинаковый коэффициент соотношения сторон к=2.