Предмет: Алгебра, автор: 5654110Asy

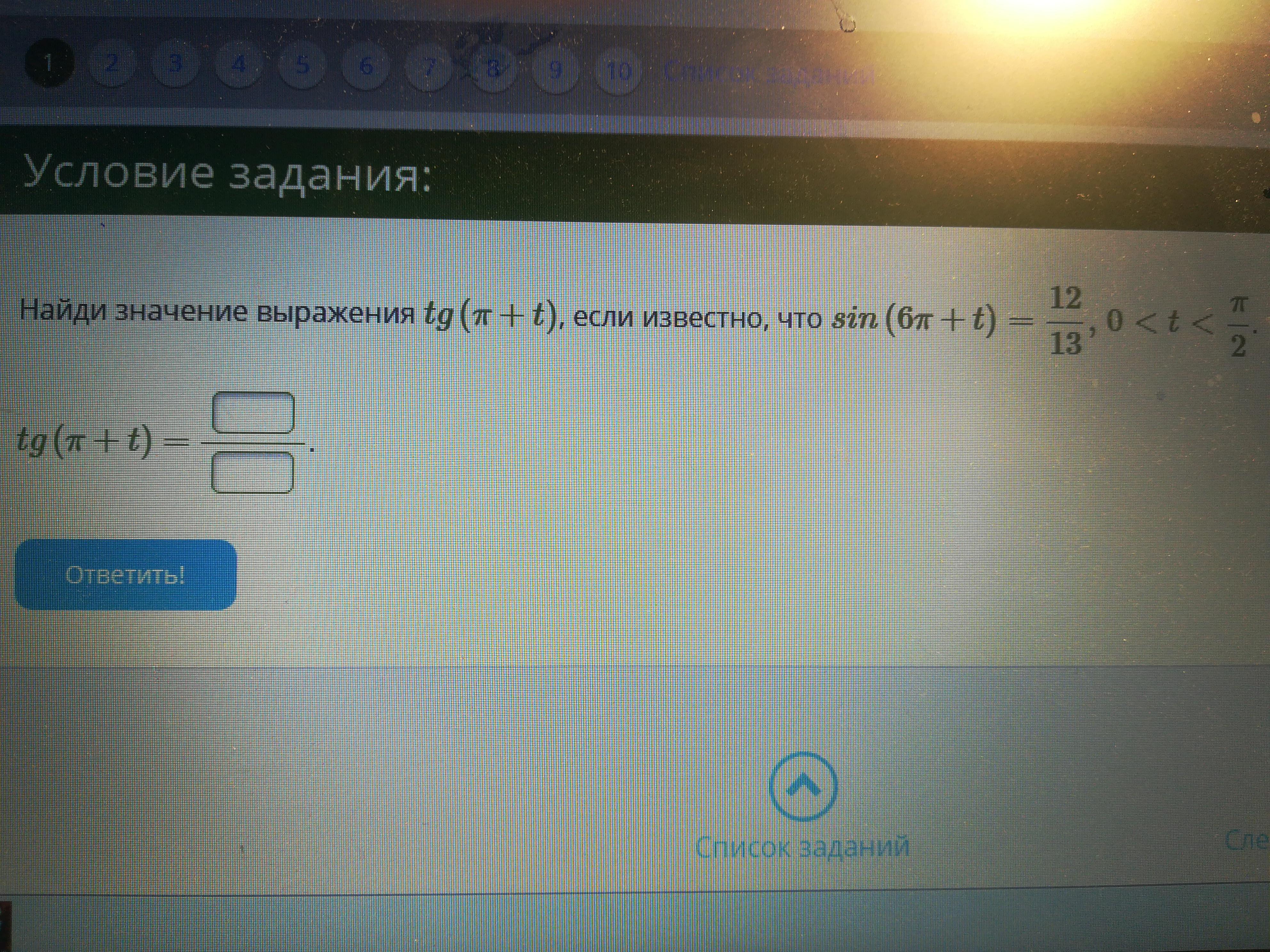
Помогите пожалуйста

Приложения:

Ответы

Автор ответа: papkovkirill

tg(pi+t)=tg(t)
sin(6pi+t)=sin(t)
$\cos(t ) = \sqrt{1 - \sin(t) {}^{2} }$
$\cos(t) = \frac{5}{13}$
$\tan(t) = \frac{ \sin(t) }{ \cos(t) }$
$\tan(t) = \frac{12}{13} \div \frac{5}{13} = \frac{12}{5} = 2.4$

annahovsepyan200391: tg(pi+t)=tg(t)
sin(6pi+t)=sin(t)
\cos(t ) = \sqrt{1 - \sin(t) {}^{2} }
\cos(t) = \frac{5}{13}
\tan(t) = \frac{ \sin(t) }{ \cos(t) }
\tan(t) = \frac{12}{13} \div \frac{5}{13} = \frac{12}{5} = 2.4

Автор ответа: annahovsepyan200391

tg(pi+t)=tg(t)

sin(6pi+t)=sin(t)

\cos(t ) = \sqrt{1 - \sin(t) {}^{2} }

\cos(t) = \frac{5}{13}

\tan(t) = \frac{ \sin(t) }{ \cos(t) }

\tan(t) = \frac{12}{13} \div \frac{5}{13} = \frac{12}{5} = 2.4

Предыдущий вопрос

Следующий вопрос

Интересные вопросы

Предмет: Английский язык, автор: nlk121

ПОМОГИТЕ ПОЖАЛУЙСТА!!!! СРОЧНО!!!
Соберите информацию о других памятниках исторических зданиях, которые находятся в опасности. Представьте это всему классу. Вы можете посетить сайт http: wheunesco.org и нажмите: Загрузить мировые наследия на 3D сфере.
На английском!