Предмет: Алгебра,
автор: IAMSLOVAR
решите уравнение
Найдите наименьший положительный корень, деленный на пи
Приложения:
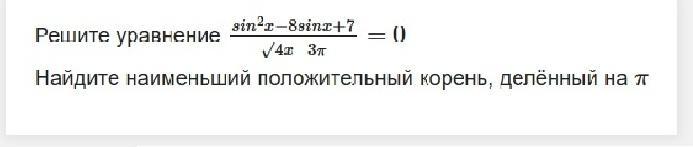
Ответы
Автор ответа:
0
Непонятно, что в знаменателе.
Дробь равна 0, если числитель равен 0,
а знаменатель отличен от 0
{sin^2x-8sinx+7=0
{√4x 3π≠0⇒ x≠ ?
Замена переменной
sinx=t
t^2-8t+7=0
D=(-8)²-4·7=64-28=36
t=(8-6)/2=1 t=(8+6)/2=7
Обратный переход
sinx=7 - уравнение не имеет корней, так как |sinx|≤1
sinx=1
x=(π/2)+2πn, n∈Z
Надо бы проверить, не будет ли знаменатель обращаться в 0.
Если не обращается, то наименьший положительный корень
x=(π/2)
О т в е т. (π/2):π=1/2
Интересные вопросы
Предмет: Русский язык,
автор: ilasikemiradziev
Предмет: Литература,
автор: dcreeop54
Предмет: Биология,
автор: kateryna250210
Предмет: Биология,
автор: nadia62
Предмет: Литература,
автор: болтливкак