Пожалуйста помогите!
В четырехугольнике две
противоположные стороны имеют равную длину, а два его противоположных угла равны 90 градусов. Докажите, что все углы этого четырёхугольника прямые.

Ответ:

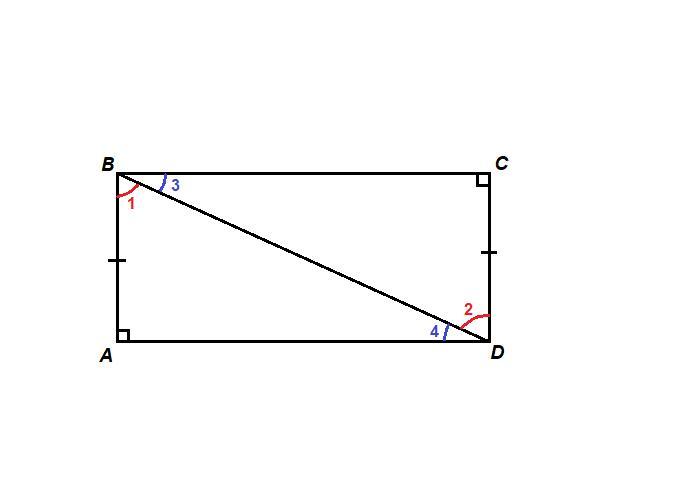
ABCD - данный четырехугольник.

∠А = ∠С = 90°

АВ = CD.

Проведем диагональ BD.

Рассмотрим треугольники ABD и CDB:

∠А = ∠С = 90°

АВ = CD - по условию,

BD - общая гипотенуза, значит

ΔABD =  ΔCDB по катету и гипотенузе.

Следовательно, ∠1 = ∠2 и ∠3 = ∠4.

____________

Сумма острых углов прямоугольного треугольника равна 90°.

Тогда ∠1 + ∠4 = 90°.

Учитывая, что ∠1 = ∠2, получаем: ∠2 + ∠4 = 90°, то есть

∠ADC = 90°.

Учитывая, что ∠3 = ∠4, получаем: ∠1 + ∠3 = 90°, то есть

∠АВС = 90°.

Значит, все углы этого четырехугольника прямые.