Боковые стороны и меньшее основание трапеции равны 10 см, а один из её углов
равен 60°. Найдите радиус окружности, описанной около этой трапеции.

Ответ:

10 см

Объяснение:

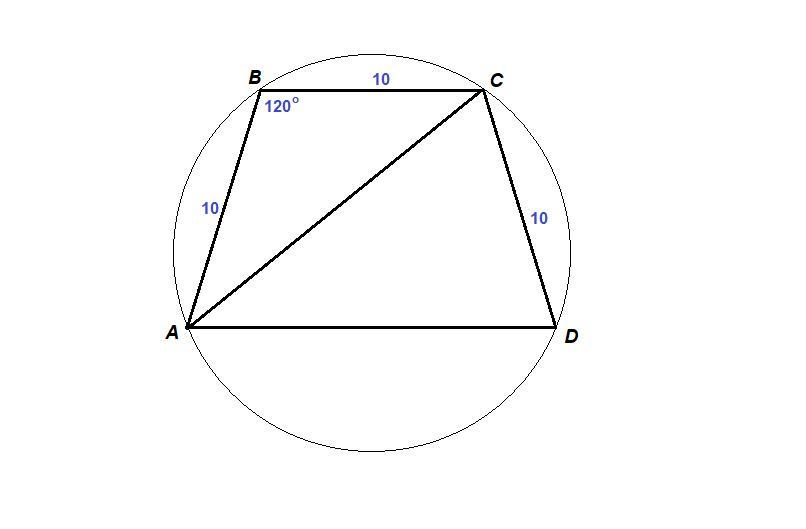
Трапеция ABCD,

АВ = ВС = CD = 10 см

∠А = 60°

Сумма углов, прилежащих к боковой стороне трапеции, равна 180° (это односторонние углы при ВС║AD и секущей АВ), значит

∠В = 180° - ∠А = 180° - 60° = 120°

Из ΔАВС по теореме косинусов:

AC² = AB² + BC² - 2·AB·BC·cos∠B

AC² = 10² + 10² - 2 · 10 · 10 · (- 1/2) =

= 100 + 100 + 100 = 300

AC = √300 = 10√3 см

ΔАВС вписан в ту же окружность, что и трапеция, поэтому достаточно найти радиус окружности, описанной около треугольника АВС:

см