помогииитеее(с объяснением)
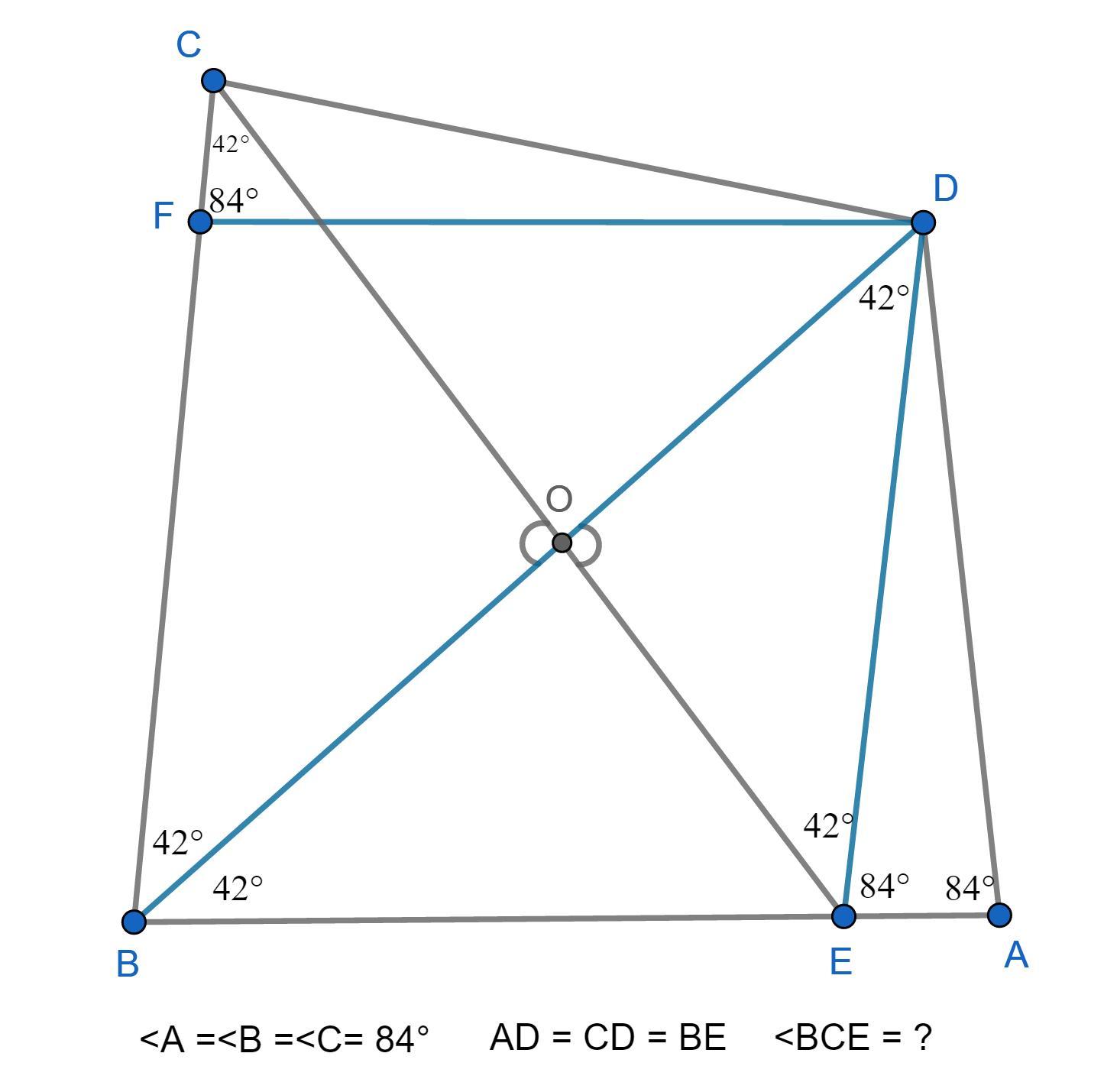
в выпуклом четырехугольнике ABCD углы при вершинах A, B и C равны по 84°. На стороне AB отмечена точка Е. Известно, что AD=CD=BE. Найдите угол BCE
Ответы
Через тч.D проведем прямую DF ║ BA. Соединим отрезком тч.D и тч.E.
∠DFC = ∠ABC = 84°, как соответствующие при DF ║ BA и CB секущей.
В ΔDFC ∠C=∠F = 84° ⇒ ΔDFC равнобедренный.
CD = FD = BE. (CD = BE по условию).
Так как FD и BE ║ и равны, то DFBE параллелограмм. ⇒ DE║FB.
∠DEA = ∠FBE = 84° как соответствующие при DE ║ FB и AB секущей.
В ΔDEA ∠E=∠A = 84° ⇒ ΔDEA равнобедренный, DE=DA = BE (DA = BE по условию).
⇒ BFDE ромб, ∠FBE = FDE = 84°, его диагональ BD является биссектрисой этих углов. ∠BDE = 42°.
BCDE - равнобедренная трапеция, углы при основаниях попарно равны. Тч. O является вершиной двух равнобедренных подобных треугольников.
ΔEOD подобен ΔCOB по двум углам. ∠COB = ∠EOD - вертикальные, ∠CBO = ∠ODE = 42°.
Из подобия треугольников следует равенство углов ∠BCO= ∠ODE = 42°.
∠BCE = 42°.