Предмет: Алгебра,
автор: GothAngelSinner
Решите систему уравнений а), б)]![[tex]\left \{ {{xy=1} \atop {y=-2x+2}} \right. \left \{ {{xy=8} \atop {y+1=x^{2} }} \right. [tex]\left \{ {{xy=1} \atop {y=-2x+2}} \right. \left \{ {{xy=8} \atop {y+1=x^{2} }} \right.](https://tex.z-dn.net/?f=%5Btex%5D%5Cleft+%5C%7B+%7B%7Bxy%3D1%7D+%5Catop+%7By%3D-2x%2B2%7D%7D+%5Cright.+%5Cleft+%5C%7B+%7B%7Bxy%3D8%7D+%5Catop+%7By%2B1%3Dx%5E%7B2%7D+%7D%7D+%5Cright.) [/tex]
[/tex]
NNNLLL54:
условия напиши...
а) второго уравнения нет...
это два разных уравнения..............................
в системе а) не записано УРАВНЕНИЕ...(y-2x+2) - это НЕ уравнение...
y-2x+2=0 ? y-2x=2 ? y=2x+2 ?????
Ответы
Автор ответа:
0
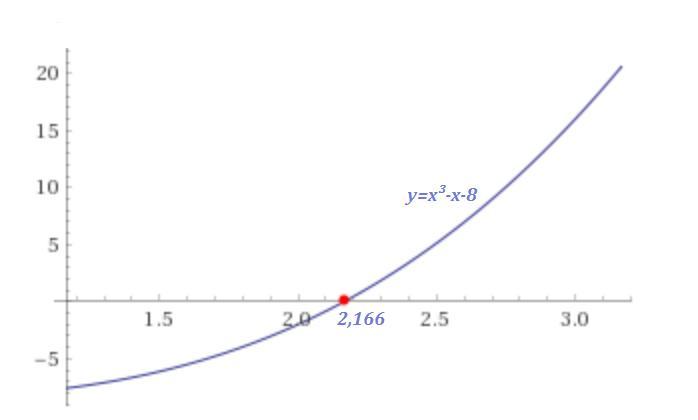
P.S. Уравнение 3 степени имеет один действительный корень (2,1663) и два комплексных ( ).
Приложения:
Интересные вопросы
Предмет: Математика,
автор: lerat364
Предмет: Математика,
автор: 6opka
Предмет: Алгебра,
автор: ttttttttttttttttt70
Предмет: Алгебра,
автор: RedWolf23
Предмет: Математика,
автор: УмнаяТагиева