В стране есть несколько городов, соединённых дорогами. Город называется захолустным, если из него выходит только одна дорога, и узловым, если из него выходит не менее трёх дорог. Известно, что в этой стране 101101101 захолустный город. При каком наименьшем количестве узловых городов можно заведомо утверждать, что в стране найдутся несколько городов, связанных циклическим маршрутом?

Ответ:

3 узловых города

Пошаговое объяснение:

Есть города, соединенные дорогами.

В некоторые города ведёт 1 дорога, это захолустные.

Всего их 1.0110.1101 = 256+64+32+8+4+1 = 365.

Ещё есть города, из которых выходит 3 дороги или больше.

Это узловые города. Надеюсь, это понятно.

Вопрос: какое минимальное количество узловых городов в стране?

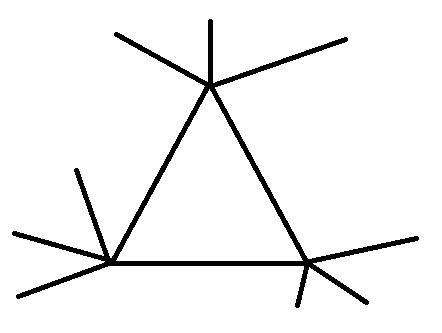
Решение: Минимальное количество узловых городов равно 3.

На рисунке показан план этого города.

Есть треугольник из 3 узловых городов, из каждого выходит много дорог.

Две дороги ведут к двум другим узловым городам, а остальные дороги ведут к захолустным городам. И всего таких захолустных дорог 365.

На рисунке показано по 3 таких дороги, выходящих из каждого узлового города к захолустным.