Предмет: Математика, автор: monolit75mail

Найти частные производные второго порядка функции многих переменных

Приложения:

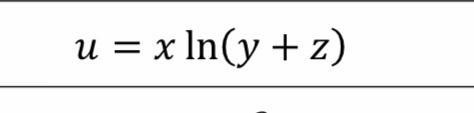
Ответы

Автор ответа: Liamus

0

$\frac{\partial u}{\partial x}=\ln(y+z),\,\frac{\partial^2 u}{\partial x^2}=0,\, \frac{\partial^2 u}{\partial x\partial y}=\frac{1}{y+z},\, \frac{\partial^2 u}{\partial x\partial z}=\frac{1}{y+z},\\\frac{\partial u}{\partial y}=\frac{x}{y+z},\, \frac{\partial^2 u}{\partial y^2}=-\frac{x}{(y+z)^2},\,\frac{\partial^2 u}{\partial y\partial x}=\frac{\partial^2 u}{\partial x\partial y}=\frac{1}{y+z},\,\frac{\partial^2 u}{\partial y\partial z}=-\frac{x}{(y+z)^2},$

$\frac{\partial u}{\partial z}=\frac{x}{y+z},\, \frac{\partial^2 u}{\partial z^2}=-\frac{x}{(y+z)^2},\,\frac{\partial^2 u}{\partial z\partial x}=\frac{\partial^2 u}{\partial x\partial z}=\frac{1}{y+z},\,\frac{\partial^2 u}{\partial z\partial y}=\frac{\partial^2 u}{\partial y\partial z}=-\frac{x}{(y+z)^2},$

Предыдущий вопрос

Следующий вопрос

Интересные вопросы

Предмет: Другие предметы, автор: huseyjvglvd

ПОМОГИТЕ ПОЖАЛУЙСТА ДАМ 20 БАЛЛОВ

5 лет назад

Предмет: История, автор: mariagorstka09

1) Высказывания историков и публицистов об Иване Грозном и результатах его правления.
2) Почему оценки этого исторического деятеля столь противоречивы?
3) Почему распространяется версия "двух Иванов Грозных" (первой и второй половине правления)?

5 лет назад

Предмет: Математика, автор: Blackiyyy

Реши уравнение: 4(0,25x - 1) = 2(x + 0,5)

5 лет назад

Предмет: Математика, автор: darkorbit19990

Заданы координаты вершин треугольника А1(-2;5), А2(1;-3), А3(4;2). Составить уравнение прямой, лежащей на стороне А1А3. Составить уравнение прямой, на которой расположена высота, проведенная к стороне А1А3. Найти точку пересечения медиан треугольника.

9 лет назад

Предмет: Математика, автор: rtr561

tg(-9x)=1 тригонометрия решите

9 лет назад