отметьте условно сходящиеся ряды.
помогите решить пожалуйста:)​

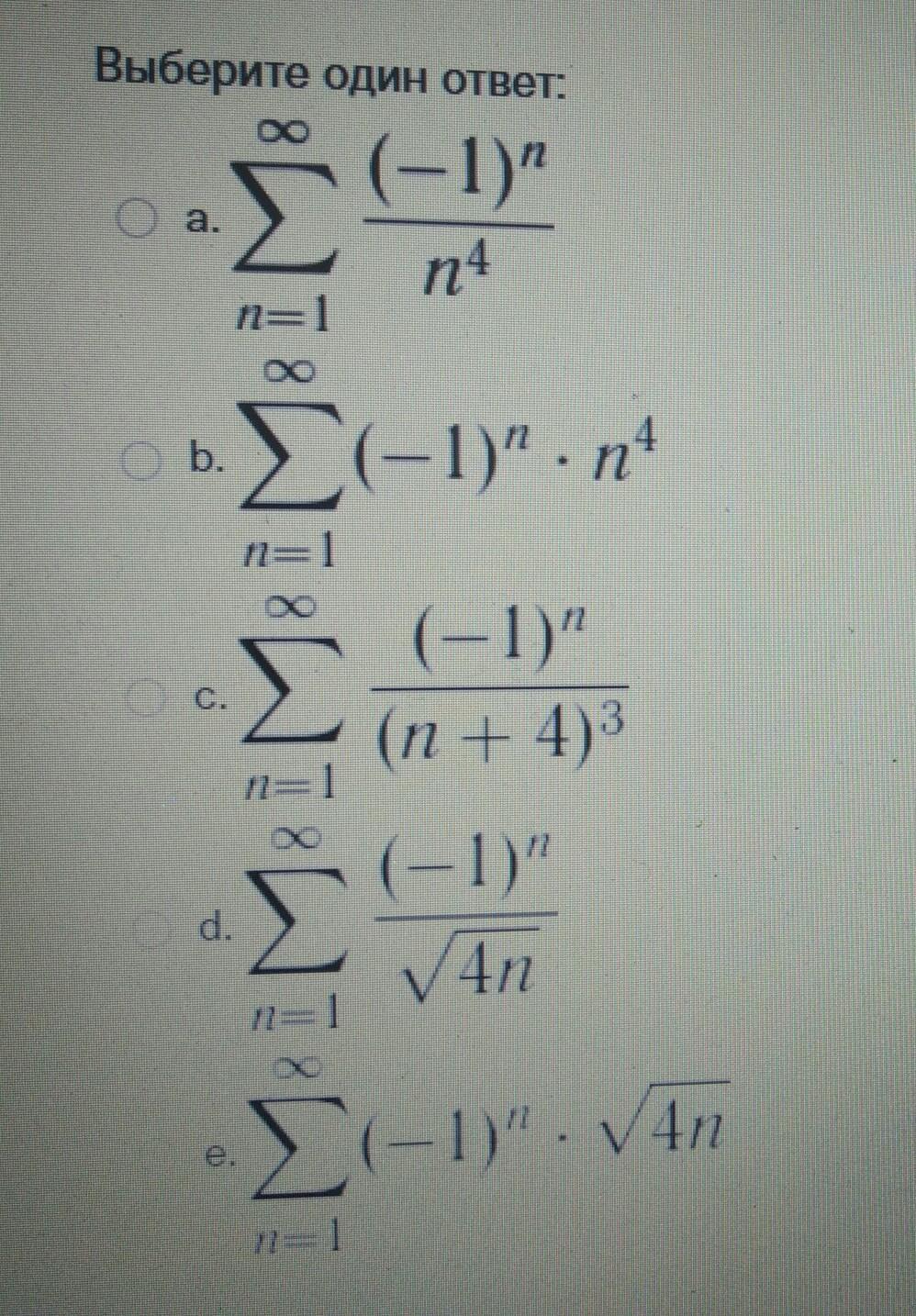
antonovm: все так , только у гармонического ряда а(n) = 1/n , а для расходимости ряда 1/sqrt(n) можно использовать известную теорему о том , что ряд с общим членом 1/ (n^p) сходится , если р > 1 и расходится , если p < = 1 , справедливость этого утверждения следует из интегрального признака сходимости

HSS9860: Решение носило чисто практический характер, предельный признак сравнения подробно не расписывался.

antonovm: но ряд , который вы называете гармоническим , таковым не является

HSS9860: Точная формулировка - "обобщённый гармонический ряд" - это как раз из теории, решение же носило сугубо практическую направленность.

HSS9860: Скорее всего у инициатора и читающих возникнет состояние диссонанса/коллизии от таких антиномий при разборе, поэтому в случае возражения/несогласия жмите "Отметить нарушение", а модераторы своё дело знают.