Предмет: Математика, автор: Santa200207

Помогите с решением дифференциального уравнения и задачи Коши.

Приложения:

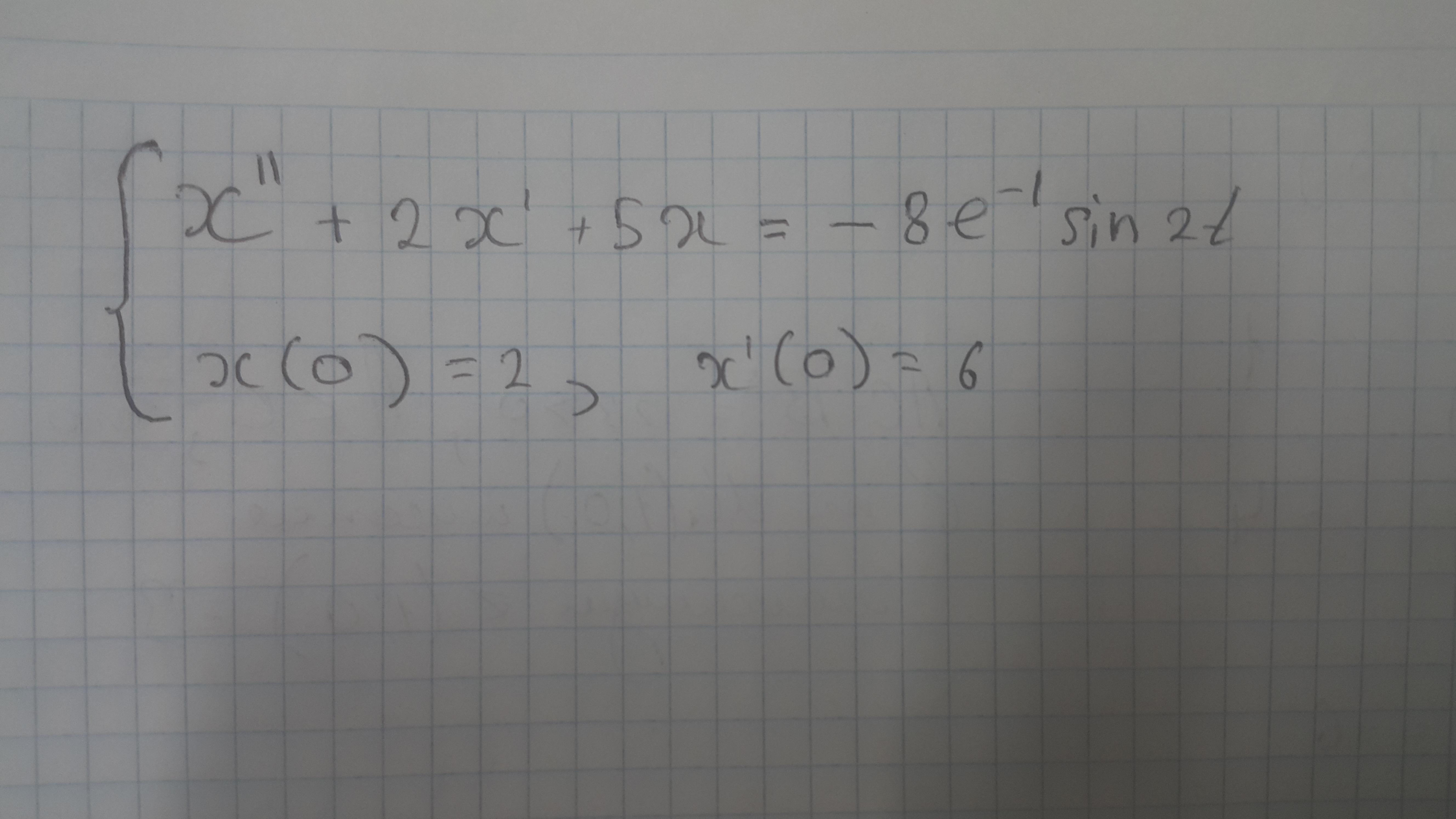
Ответы

Автор ответа: Аноним

Найдем сначала общее решение соответствующего однородного дифференциального уравнения:

$x''+2x'+5x=0$

Используя замену $x'=e^{kt}$ , получим характеристическое уравнение

$k^2+2k+5=0$

$k=-1\pm 2i$

Общее решение однородного дифференциального уравнения:

$x^*=C_1e^{-t}\cos 2t+C_2e^{-t}\sin 2t$

Рассмотрим функцию: $f(t)=-8e^{-1}\sin 2t$ . Здесь $P_n(t)=-8e^{-1}$ откуда $n=0;$ и $\alpha=0;~\beta=2;~~~Q_n(t)=0$ . Сравнивая α, β с корнями характеристического уравнения, частное решение будем искать в виде:

$x^{**}=A\sin 2t+B\cos 2t\\ x'=(A\sin2t+B\cos 2t)'=2A\cos 2t-2B\sin 2t\\ x''=(2A\cos 2t-2B\sin 2t)'=-4A\sin2t-4B\cos 2t$

Подставляем в исходное дифференциальное уравнение:

$-4A\sin2t-4B\cos 2t+4A\cos2t-4B\sin2t+5A\sin2t+5B\cos2t=-8e^{-1}\sin2t$

$A\sin2t+B\cos2t+4A\cos2t-4B\sin2t=-8e^{-1}\sin2t\\ \\ \sin2t(A-4B)+\cos 2t(B+4A)=-8e^{-1}\sin 2t$

Приравниваем коэффициенты при cos2x и sin2x, получаем систему:

$\displaystyle \left \{ {{A-4B=-8e^{-1}} \atop {B+4A=0}} \right.~~~\Rightarrow~~~\left \{ {{A+16A=-8e^{-1}} \atop {B=-4A}} \right.~~~\Rightarrow~~~\left \{ {{A=-\frac{8}{17}e^{-1}} \atop {B=\frac{32}{17}e^{-1}}} \right.$

Общее решение линейного неоднородного дифференциального уравнения:

$x=x^*+x^{**}=C_1e^{-t}\cos 2t+C_2e^{-t}\sin 2t-\frac{8}{17}e^{-1}\sin 2t+\frac{32}{17}e^{-1}\cos 2t$

Осталось решить задачу Коши, подставляя начальные условия

$x'=(C_1e^{-t}\cos 2t+C_2e^{-t}\sin 2t-\frac{8}{17}e^{-1}\sin 2t+\frac{32}{17}e^{-1}\cos 2t)'=\\ =-C_1e^{-t}\cos2t-2C_1e^{-t}\sin2t-C_2e^{-t}\sin2t+2C_2e^{-t}\cos 2t-\\ -\frac{16}{17}e^{-1}\cos2t-\frac{64}{17}e^{-1}\sin2t\\ \\ x'(0)=2;~~~2=-C_1+2C_2-\frac{16}{17}e^{-1}\\ x(0)=6;~~~~6=C_1+\frac{32}{17}e^{-1}$

$\displaystyle \left \{ {{2=-C_1+2C_2-\frac{16}{17}e^{-1}} \atop {6=C_1+\frac{32}{17}e^{-1}}} \right.~~~~\Rightarrow~~~~\left \{ {{C_2=4+\frac{8}{17}e^{-1}} \atop {C_1=6-\frac{32}{17}e^{-1}}} \right.$