Предмет: Алгебра,
автор: nictooo
начиная со 2,решите пожалуйста
Приложения:

Ответы
Автор ответа:
0
Решение на фото, если что-то не понятно - спрашивайте.
Приложения:
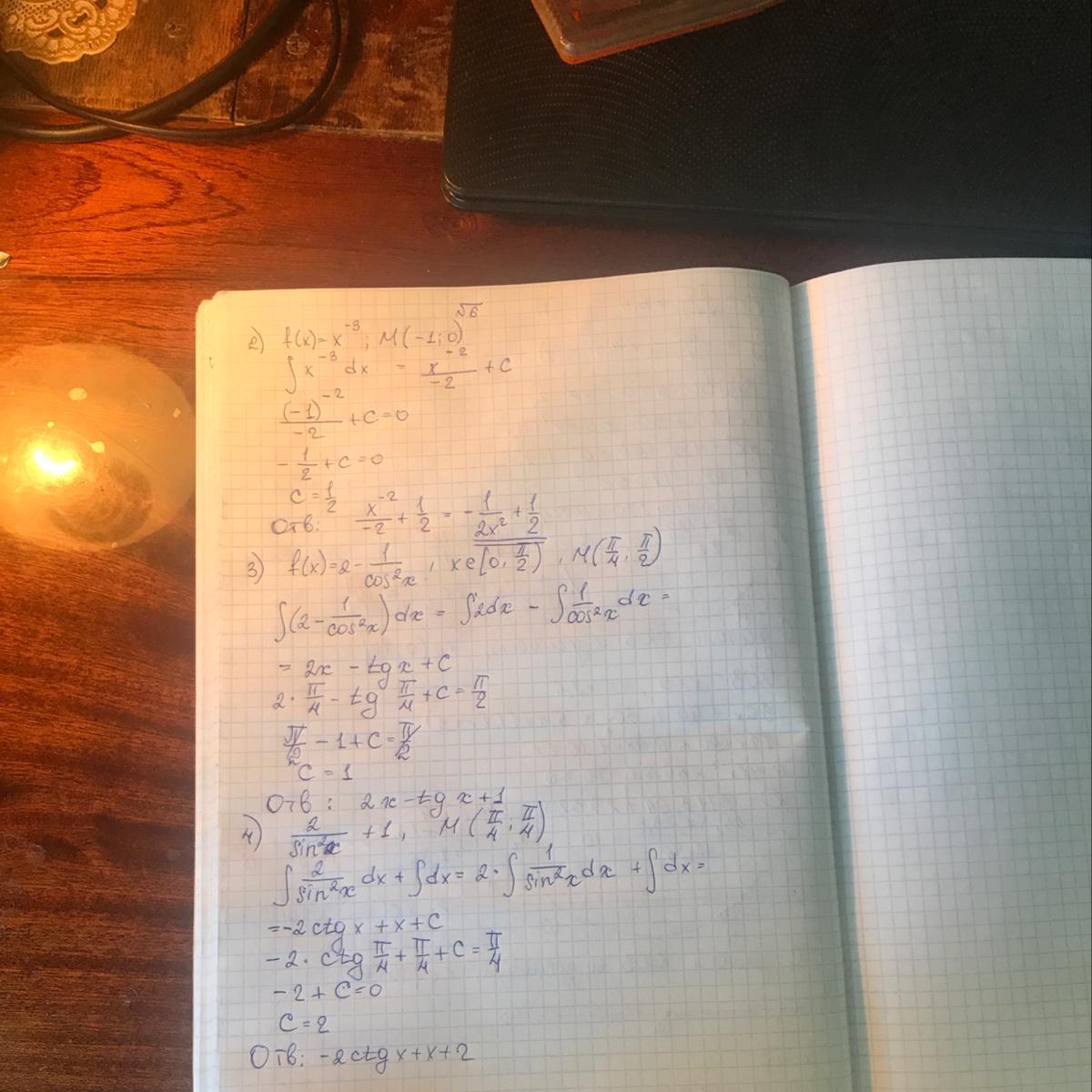
Автор ответа:
0
Ответ:
Объяснение:
Интересные вопросы
Предмет: Русский язык,
автор: strelkovakira3
Предмет: Геометрия,
автор: vaushnaakristina
Предмет: География,
автор: romandyachuk330
Предмет: История,
автор: lannastya
Предмет: Математика,
автор: ААнгелиночкАА