Предмет: Алгебра, автор: Shinimini

Решите неравенство $sin x\leq 7cosx +5$
((Вот, что пока у меня есть))

Приложения:

Аноним: надо решение по другой схеме?)

Ответы

Автор ответа: nafanya2014

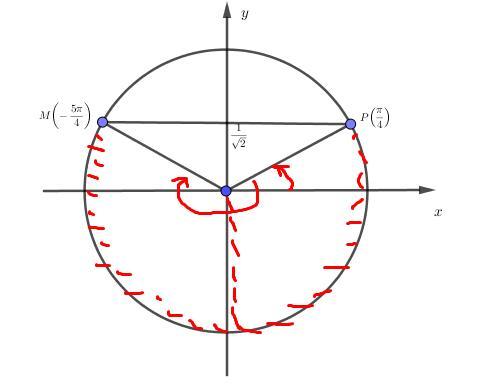
Начало см рис.

sin²(x/2)+sin(x/2)cos(x/2)-6cos²(x/2) ≤0

Слева однородное тригонометрическое выражение.

Делим на сos²(x/2)≠0

tg²(x/2)+tg(x/2)-6≤0

D=1+24=25

(tg(x/2)+3)(tg(x/2)-2)≤0

-3≤tg(x/2)≤2

arctg(-3)+πk≤(x/2)≤arctg(2)+πk, k∈Z

2arctg(-3)+2πk≤x≤2arctg(2)+2πk, k∈Z

О т в е т. -2arctg(3)+2πk≤x≤2arctg(2)+2πk, k∈Z -

Приложения:

Автор ответа: Аноним

По формуле дополнительного угла

$\sin x-7\cos x\leq 5\\ \\ \sqrt{1^2+7^2}\sin \left(x-\arcsin\frac{7}{\sqrt{1^2+7^2}}\right)\leq 5\\ \\ 5\sqrt{2}\sin \left(x-\arcsin\frac{7}{\sqrt{50}}\right)\leq 5\\ \\ \sin\left(x-\arcsin\frac{7}{\sqrt{50}}\right)\leq \frac{1}{\sqrt{2}}\\ \\ -\frac{5\pi}{4}+2\pi k\leq x-\arcsin\frac{7}{\sqrt{50}}\leq\frac{\pi}{4}+2\pi k,k \in \mathbb{Z}\\ \\ \\ \boxed{\boldsymbol{\arcsin\frac{7}{\sqrt{50}}-\frac{5\pi}{4}+2\pi k\leq x\leq \frac{\pi}{4}+\arcsin\frac{7}{\sqrt{50}}+2\pi k,k \in \mathbb{Z}}}$