Помогите с решением 26-ой задачи, пожалуйста
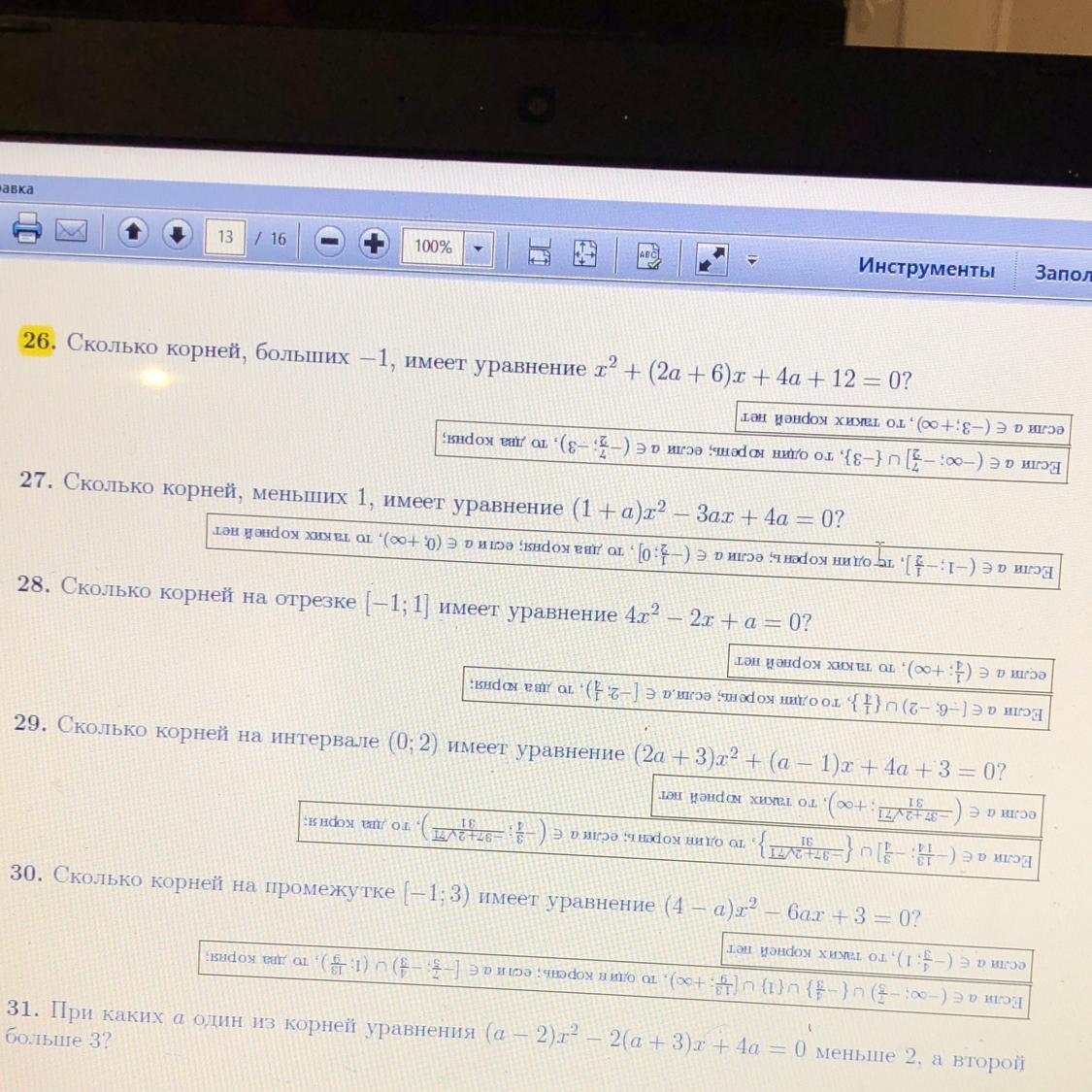
Ответы
Графиком функции y=x²+(2a+6)x+4a+12 является парабола, ветви которой направлены вверх.
D=(2a+6)^2-4(4a+12)=(2(a+3))^2-4*4(a+3)=4(a+3)(a+3-4)=4(a+3)(a-1)
Если D < 0 уравнение не имеет корней, т.е при -3 < a < 1
Если D=0, т.е при a =-3; a=1 уравнение имеет один корень
При a=-3 уравнение принимает вид: х²=0 ;
и корень х=0 больше (-1)
При a=1 уравнение
x²+8x+16=0
(x+4)²=0
х=-4 корень не удовлетворяет требованию задачи.
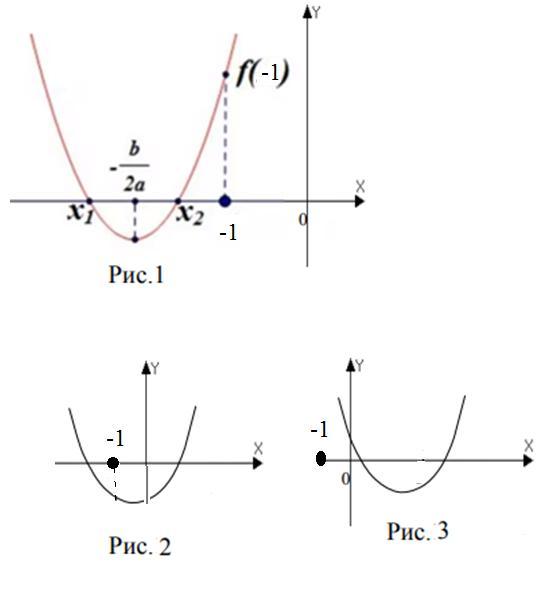
Если D>0, т.е. при a < -3 или a>1 уравнение имеет два корня и потому возможны три случая расположения параболы в системе координат ( см. рис.) по отношению к (-1)
В первом случае оба корня левее (-1), т. е оба корня меньше -1
{D>0 ⇒a < -3 или a > 1
{f(-1)>0⇒ (-1)²+(2a+6)(-1)+4a+12 >0 ⇒2a+7>0 ⇒a > -7/2
{x(вершины) < - 1 ⇒ - a - 3 < -1⇒ a > -2
a ∈ (1;+∞)
Во втором случае (-1) расположена между корнями, т. е один корень меньше (-1), второй больше (-1)
Это соответствует условию:
{f(-1) < 0⇒ 2a+7 < 0 ⇒a < -3,5
В третьем случае оба корня больше (-1), что соответствует условиям
{D>0 ⇒ a < -3 или а > 1
{f(-1)>0 ⇒2a+7 >0 ⇒a>-3,5
{x(вершины) > -1 ⇒ a < -2
a∈(-7/2;-3)
О т в е т.
при a∈(-∞;-3,5)U{-3} - один корень
при а∈(-3,5;-3)- два корня
при а∈(-3;1)U{1}U(1;+∞)=(-3;+∞) нет корней