Предмет: Алгебра,
автор: grww84
Срочно, помогите. Алгебра 11 класс. Даю 30 баллов.
Приложения:
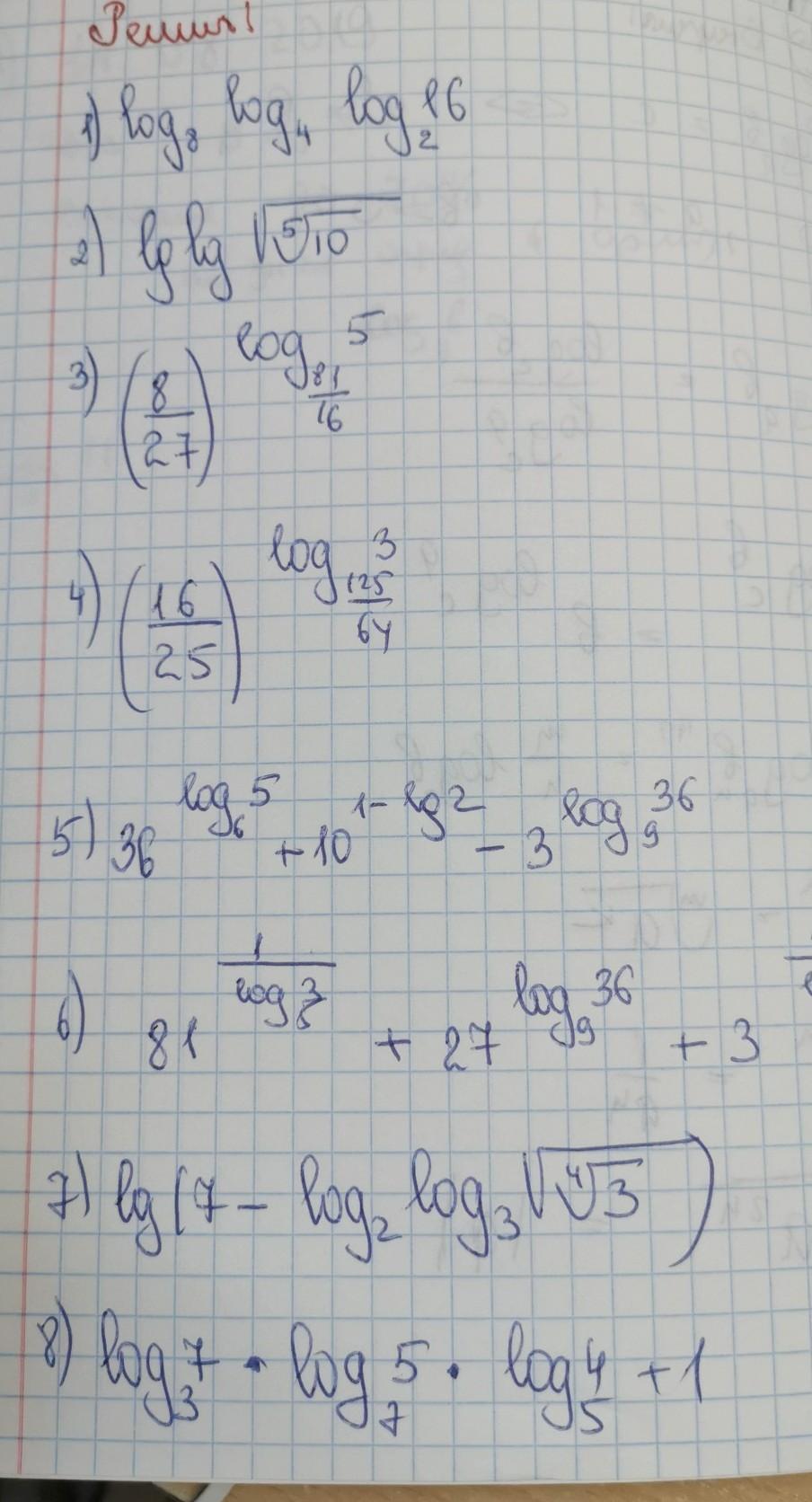
Ответы
Автор ответа:
1
Объяснение:
Интересные вопросы
Предмет: Математика,
автор: yevgeniyademchenko
Предмет: Биология,
автор: natalaspesivceva16
Предмет: Математика,
автор: agleeva15
Предмет: Физика,
автор: КириллНельсон