Предмет: Математика, автор: AlineLightning

Дано: ctg(x) =2

Найти: (sin^4(x)+5sin^3(x)×cos(x)-cos^4(x) )/2sin^2(x)-3cos^2(x)

Приложения:

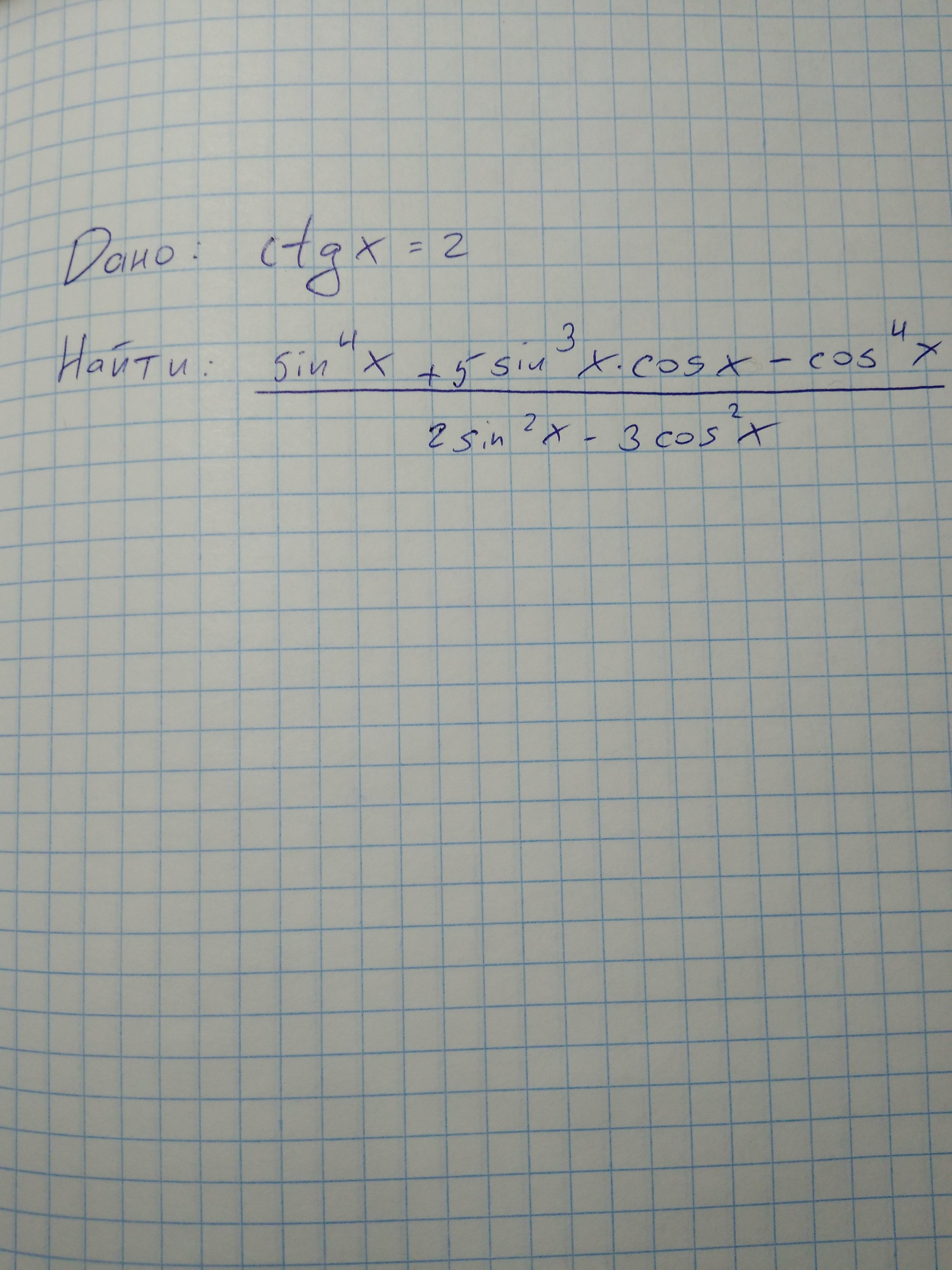
Ответы

Автор ответа: NNNLLL54
1

ctgx=2\\\\\frac{sin^4x+5sin^3x\, cosx-cos^4x}{2sin^2x-3cos^2x}=\frac{sin^4x\cdot (1+5\cdot \frac{cosx}{sinx}-\frac{cos^4x}{sin^4x})}{2(1-cos^2x)-3cos^2x}=\frac{sin^4x\cdot (1+5\, ctgx-ctg^4x)}{2-5\, cos^2x}=\\\\=\frac{sin^4x\cdot (1+5\cdot 2-2^4)}{sin^2x\cdot (\frac{2}{sin^2x}-5\cdot \frac{cos^2x}{sin^2x})}=\frac{sin^2x\cdot (-5)}{2\cdot (1+ctg^2x)-5\cdot ctg^2x}=\frac{\frac{1}{1+ctg^2x}\cdot (-5)}{2\cdot (1+4)-5\cdot 4}=\\\\\\=\frac{-\frac{5}{5}}{-10}=\frac{1}{10}=0,1

Автор ответа: Аноним
0

Решение и ответ смотри во вложении

Приложения:
Предыдущий вопрос
Следующий вопрос
Интересные вопросы
Предмет: Алгебра, автор: Letoya0
сто баллов. голову сломала. 9а2+30авс+25в2с2, нужно представить в виде квадрата двучлена. четыре варианта:
а) (3а+5вс)2
б) то же, но наоброт
в)(-5в+3ас)2
г)(5вс+3а)2
5 лет назад
Предмет: Биология, автор: jenek008
10. Какие утверждения верны? 1. У крота плоские передние лапы с большими когтями, так как он живет в почве. 2. Ноги животных в водной среде приспособлены к бегу, прыжкам. А. верно только 1. Б. верно только 2. В. оба утверждения верны г. оба утверждения неверны
​
5 лет назад
Предмет: Литература, автор: mrizo5253
Составить синквейн на тему Добро
5 лет назад
Предмет: Биология, автор: СоняОльховская
на варенье иногда можно наблюдать плесень зеленого цвета может ли она фотосинтезировать Дайте аргументированный ответ
9 лет назад
Предмет: История, автор: Аноним
какие цели преследовали латинской Америки с США?
9 лет назад