Предмет: Математика, автор: irinshapov

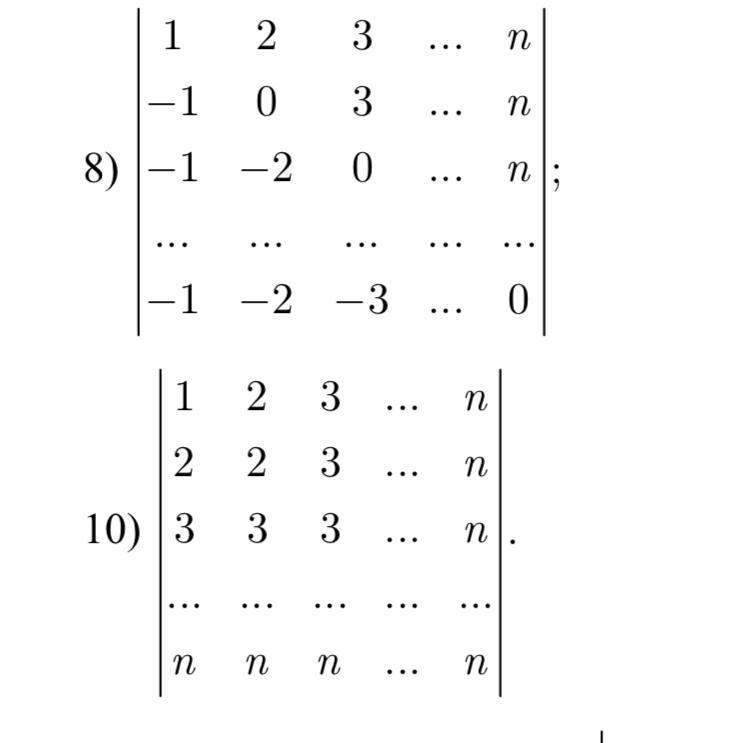
Помогите найти определитель матрицы. Срочно, пожалуйста!

Приложения:

Ответы

Автор ответа: axatar

Ответ:

8) 1·2·3·...·n=n!

10) n

Пошаговое объяснение:

Используем свойство определителя:

Определитель не изменится, если к элементам какого-либо столбца (строки) прибавить соответствующие элементы другого столбца умноженного на одно и тоже число.

8) $\left[\begin{array}{ccccc}1&2&3&...&n\\-1&0&3&...&n\\-1&-2&0&...&n\\ ...&...&...&...&...\\-1&-2&-3&...&0\end{array}\right]$ =

= $\left[\begin{array}{ccccc}1&2&3&...&n\\0&2&6&...&2n\\0&0&3&...&2n\\ ...&...&...&...&...\\0&0&0&...&n\end{array}\right]$ =

=1·2·3·...·n=n!

10) $\left[\begin{array}{ccccc}1&2&3&...&n\\2&2&3&...&n\\3&3&3&...&n\\ ...&...&...&...&...\\n&n&n&...&n\end{array}\right]$ =

= $\left[\begin{array}{ccccc}1&2&3&...&n\\1&0&0&...&0\\2&1&0&...&0\\ ...&...&...&...&...\\n-1&n-2&n-3&...&0\end{array}\right]$ =

= $\left[\begin{array}{ccccc}1&2&3&...&n\\1&0&0&...&0\\0&1&0&...&0\\ ...&...&...&...&...\\0&0&...&1&0\end{array}\right]$ =

$=n\left[\begin{array}{ccccc}1&0&0&...&0\\0&1&0&...&0\\0&0&1&...&0\\...&...&...&...&...\\0&0&0&...&1\end{array}\right]$ =

=n·1=n

Предыдущий вопрос

Следующий вопрос

Интересные вопросы

Предмет: Физика, автор: patosch777

конспект на:электрический ток в жидкостях

5 лет назад

Предмет: Алгебра, автор: desize13

Помогите по алгебре пожалуйста

5 лет назад

Предмет: Английский язык, автор: whshsh04

ПОМОГИТЕ ПОЖАЛУЙСТА Английский 70 баллов

5 лет назад

Предмет: Математика, автор: деткагецмер

как дегко делить и умножать 3 значение числа

9 лет назад

Предмет: Математика, автор: mirzoevaz33

в одном бидоне было 35 л воды ,сначала из него вылили 7 л воды потом оставшуюся воды разлили в ведра ,по 4 л в каждое сколько ведер понадобилось

9 лет назад