Предмет: Алгебра, автор: Аноним

прошу,помогите. алгебра 11 класс. пределы.

Приложения:

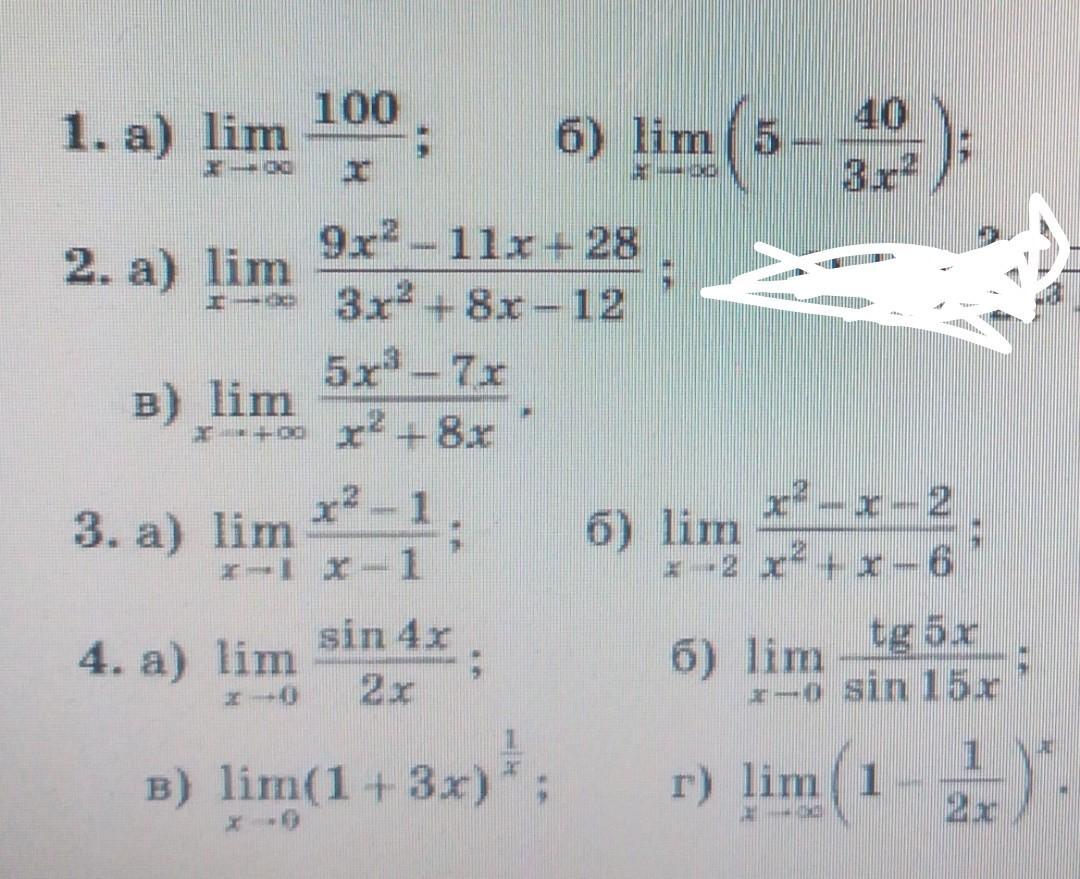
NNNLLL54: много примеров в одном вопросе...

Аноним: Не получится получить решение?

Ответы

Автор ответа: NNNLLL54

1

$1a)\; \; \lim\limits _{x \to \infty}\frac{100}{x}=\frac{100}{\infty }=0\\\\1b)\; \; \lim\limits _{x \to \infty}(5-\frac{40}{3x^2})=5-\frac{40}{\infty }=5-0=5\\\\\\2a)\; \; \lim\limits _{x \to \infty}\frac{9x^2-11x+28}{3x^2+8x-12}=\lim\limits _{x \to \infty}\frac{9x^2}{3x^2}=\frac{9}{3}=3\\\\2b)\; \; \lim\limits _{x \to \infty}\frac{5x^3-7x}{x^2+8x}=\lim\limits _{x \to \infty}\frac{5x^3}{x^2}=\lim\limits _{x \to \infty}\, (5x)=5\cdot \infty =\infty$

$3a)\; \; \lim\limits _{x \to 1}\frac{x^2-1}{x-1}=\lim\limits _{x \to 1}\frac{(x-1)(x+1)}{x-1}=\lim\limits _{x \to 1}\, (x+1)=1+1=2\\\\3b)\; \; \lim\limits _{x \to 2}\frac{x^2-x-2}{x^2+x-6}=\lim\limits _{x \to 2}\frac{(x-2)(x+1)}{(x-2)(x+3)}=\lim\limits _{x \to 2}\frac{x+1}{x+3}=\frac{2+1}{2+3}=\frac{3}{5}$

$4a)\; \; \lim\limits _{x \to 0}\frac{sin4x}{2x}=\lim\limits _{x \to }\frac{4x}{2x}=2\\\\4b)\; \; \lim\limits _{x \to 0}\frac{tg5x}{sin15x}=\lim\limits _{x \to 0}\frac{5x}{15x}=\frac{5}{15}=\frac{1}{3}\\\\4c)\; \; \lim\limits _{x \to 0}(1+3x)^{\frac{1}{x}}=\lim\limits _{x \to 0}\Big ((1+3x)^{\frac{1}{3x}}\Big )^{\frac{3x}{x}}=e^{\lim\limits _{x \to 0}\frac{3x}{x}}=e^3\\\\4d)\; \; \lim\limits _{x \to \infty}(1-\frac{1}{2x})^{x}=\lim\limits _{x\to \infty }\Big ((1+\frac{-1}{2x})^{-2x}\Big )^{\frac{x}{-2x}}=e^{-\frac{1}{2}}$

Автор ответа: Аноним

1

Ответ и объяснение во вложении

Приложения:

Предыдущий вопрос

Следующий вопрос

Интересные вопросы

Предмет: Математика, автор: litvinovaanzela923

Прочитайте текст та виконайте завдання. 508 Людина і дроби тісно пов'язані між собою: 55 маси тіла люди- 50 25 ни становить кров; всієї крові міститься в кровоносних су- 10 5 динах; 50 у печінці; 50 у селезінці; 50 у підшкірних судинах, 50 л крові виштовхується за одне скорочення серця. (1) Випишіть усі звичайні дроби, які зустрічаються в тексті. Впорядкуйте їх за зростанням. (2) Скоротіть дроби, які можливо скоротити. (3) Знайдіть масу крові людини вагою 100 кг. (4) Порівняйте на скільки більше крові у печінці, ніж у у селезінці.

5 лет назад

Предмет: Другие предметы, автор: Аноним

Что не вместится даже в самую большую кастрюлю?

Загадки на логику.

5 лет назад

Предмет: Литература, автор: dasha9631

сообщение на тему Джек Лондон на Аляске.
пожалуйста

5 лет назад

Предмет: Математика, автор: крутойябыл

какое число надо поделить на 25 и на 36 чтобы не было остатка?

9 лет назад

Предмет: Биология, автор: лика20042

какие слои видны на поперечном срезе стебля при рассматривании невооруженным глазом и с помощью микроскопа

9 лет назад