Предмет: Алгебра, автор: notfullina

Решите интеграл по частям

Приложения:

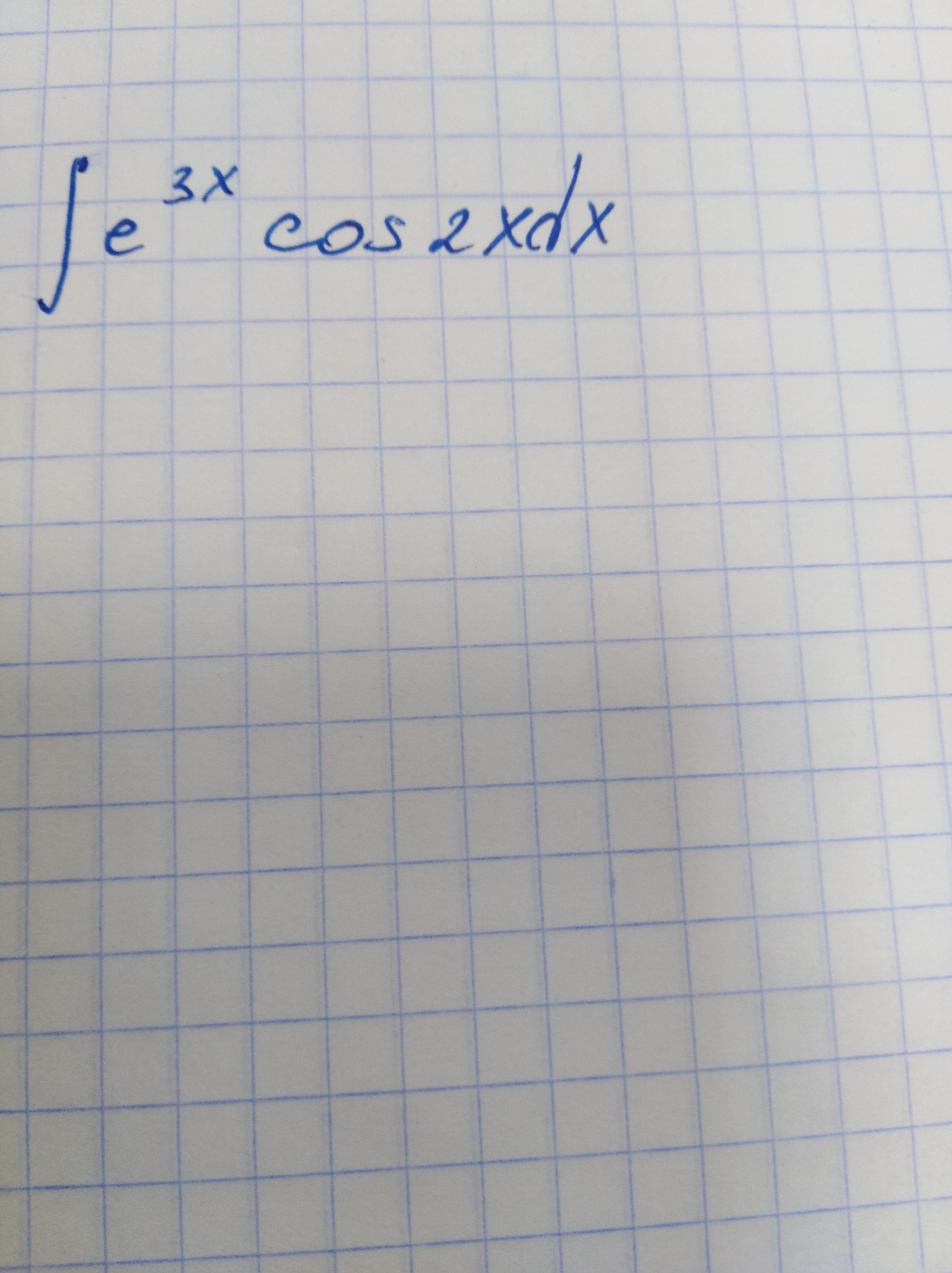
Ответы

Автор ответа: ProGroomer

0

Ответ:

$\int e^{3x}cos 2x dx={9\over39}e^{3x}cos2x+\frac{18}{117}e^{3x}sin2x$

Объяснение:

Формула:

$\int {u} \, dv=uv-\int {v} \, du$

$\int e^{3x}cos 2x dx = \{u=cos2x, dv=e^{3x}\Rightarrow v= {e^{3x}\over3}, du=-2sin2x\}=\\={1\over3}e^{3x}cos2x+{2\over3}\int e^{3x}sin2x dx=\{u=sin2x, dv=e^{3x} \Rightarrow v={e^{3x}\over3},du=2cos2x\}={1\over3}e^{3x}cos2x+{2\over9}e^{3x}sin2x -{4\over9}\int e^{3x}cos 2x dx\\\\\int e^{3x}cos 2x dx={1\over3}e^{3x}cos2x+{2\over9}e^{3x}sin2x -{4\over9}\int e^{3x}cos 2x dx\\\\\frac{13}{9}\int e^{3x}cos 2x dx={1\over3}e^{3x}cos2x+{2\over9}e^{3x}sin2x\\\\$

$\int e^{3x}cos 2x dx={9\over39}e^{3x}cos2x+\frac{18}{117}e^{3x}sin2x$

Предыдущий вопрос

Следующий вопрос

Интересные вопросы

Предмет: Алгебра, автор: AndreyClassB

100 баллов срочно АЛГЕБРА

5 лет назад

Предмет: Математика, автор: rio775

Найти площадь плоской фигуры, ограниченной кривыми с пояснениями
y+x=0, y=2x-x^2

5 лет назад

Предмет: Математика, автор: amigo2009gg

3.Решите системы уравнений:
способом сложения 5х + 3 = 7 2x-9y=-38

5 лет назад

Предмет: Математика, автор: 20238

найдите наименьшее общее кратное чисел удобным спбом.5.16и20. 15.30и45. 10.14и35.

9 лет назад

Предмет: Литература, автор: shavkatovs89gmailcom

Как умер М.Ю.Лермонтов

9 лет назад